Alex Barnett

PHYSICS RESEARCH

HELLER GROUP 1996-2000

 slightly scary photo of me How to reach me (if you could go backwards in time):
Lyman 429, tel (617) 496-4013.

By physical mail:
Department of Physics
Harvard University
Jefferson Labs, 17a Oxford St
Cambridge MA, 02138, USA.

...go home.

In October 2000 I graduated from Rick Heller's research group at the Harvard Physics Department. Rick's group specializes in quantum chaos, theoretical chemistry, and numerical methods.

More about research topics...

Use some computer codes I have wrote during this time...

somebody else playing billiards

General introduction

My work involves the quantum mechanics of non-interacting particles trapped in a classically-chaotic cavity, or `billiard', with hard walls. The problem is identical to that of the wave motion of an elastic sheet stretched across a drum-head. It is very important to find the eigenstates (vibrational modes) and how they change when the cavity is deformed - for instance, how large can a deformation be before the states are scrambled? Computationally it is hard, even in only two dimensions, to find states with high quantum numbers (up to a million states above the ground state) - some of my research has been developing efficient methods for this. As well as being a paradigm for quantum chaos (the study of quantum mechanics in chaotic systems), such hard-walled systems can model `quantum dots' (2D electron gases in semiconductor microstructures), nucleon motion in a deformed nucleus (3D fermion gas), light trapped in chaotic optical fibers ...any system governed by the Helmholtz equation.

If the cavity slowly changes shape, the particles can be heated in an irreversible manner due to random energy exchange with the moving walls - this dissipation happens in both quantum and classical mechanics. In work with Doron Cohen, we have discovered the fact that deformations which preserve shape have vanishing heating rates, and this led us to improve the `wall formula' estimate for heating rate. The dilation deformation case turns out to be crucial to the operation of an efficient numerical eigenstate method too.

I also study open systems: the conductance of electron or matter waves through arbitrary potential structures, for instance a quantum point contact coupled to an open resonant cavity. A scattering theorist's approach provides many insights which complement the traditional transmission matrix recipe (Landauer formula).

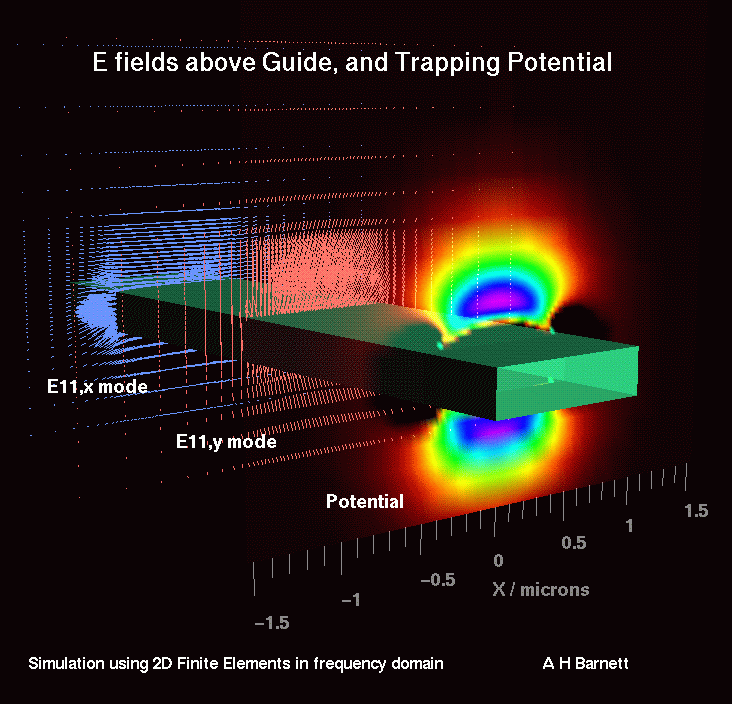
I have also designed and simulated a new neutral atom waveguide, which uses the evanescent light field above a submicron dielectric optical guide. This design is ideal for the exciting experimental field of atom optics
`on a chip' (substrate). This also involved numerical 2D eigenstate calculations - vector electromagnetic waves rather than scalar waves.

Research in the Heller Group is always interactive, exciting and full of variety, mainly due to Rick Heller's own highly intuitive and non-competitive research atmosphere, and his constant flow of good ideas!

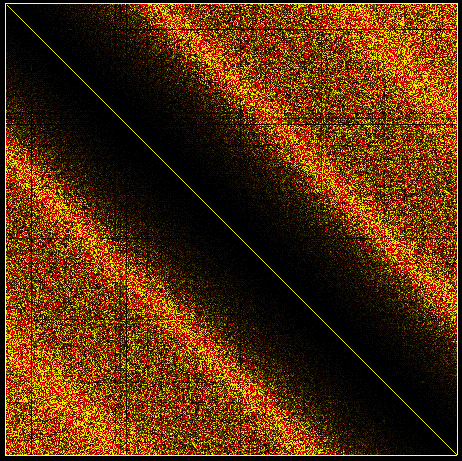
dilation matrix in energy basis: red positive, yellow negative, black zero.

PARAMETER-DEPENDENT DEFORMATION OF CHAOTIC QUANTUM BILLARDS

A single particle trapped inside certain hard-walled cavities, in which the classical motion is chaotic, has been a prototype system for studying `quantum chaos' in the last 20 years.

The rate of change of the hamiltonian with respect to a certain deformation of the billiard boundary forms a matrix M when written in the undeformed eigenbasis. The band profile (mean square matrix element as a function of distance away from the diagonal) of M has physical significance: it tells you the dissipation coefficient under periodic time-depenedent `driving' of the boundary, in the linear response regime (classically, and when this is a valid regime, quantum-mechanically too, see this).  Also the local density of avoided crossings (for 1 deformation parameter), and diabolical points (degeneracies in the spectrum for 2 or more parameters), are directly related to the limit of the band profile close to the diagonal. I hope to extend the work of Berry, Wilkinson and Austin on diabolical points in real billiard systems (as opposed to random matrices). Note that avoided crossings also are a mechanism for (quantum) dissipation - however an entirely different one than linear response mentioned above.

Above I show M in the case of the deformation being dilation. Contrast this with M for a `generic', ie non-special, deformation (a wiggle along the boundary), shown here. (Both data are for the quarter stadium billiard, for all 451 eigenstates in the wavevector range 398 < k < 402). The special property that for dilation, the mean square matrix element vanishes as you approach the diagonal has been called quasi-orthogonality. It is the key to the method of Vergini & Saraceno (see below). Using a technique of Mario Feinberg, the mean square element can be estimated semiclassically, using a long classical trajectory. We have found that the special cases of dilation and translation have a 4th power law, and rotation a 2nd power law, for the mean square element as a function of distance from the diagonal. This result applies to a generic billiard - we see deviations from these power laws (or possibly very slow convergence) in the stadium billiard, we believe due to neutrally-stable orbits causing long-time correlations.

For more detail, see complete slides for my 3rd Feb 2000 group talk on this, or the paper (nlin.CD/0003018) on this work with Doron Cohen and Rick Heller.

generalized Sinai billiard in 2DIMPROVED `WALL FORMULA' FOR DISSIPATION RATE OF A DRIVEN CHAOTIC BILLIARD

We consider the response of a chaotic cavity in d dimensions to periodic driving.  We are motivated by older studies of one-body dissipation in nuclei, and also by anticipated mesoscopic applications.  For calculating the rate of energy absorption due to time-dependent deformation of the confining potential, we introduce an improved version of the wall formula. Our formulation takes into account that a special class of deformations causes no heating in the zero-frequency limit.  We also derive a mesoscopic version of the Drude formula, and explain that it can be regarded as a special example of our calculations.  Specifically we consider a quantum dot driven by electro-motive force which is induced by a time-dependent homogeneous magnetic field.
This work is in collaboration with Doron Cohen and Rick Heller. Download our paper... Rate of energy absorption for a driven chaotic cavity (nlin.CD/0006041).

piece of stadium eigenstateVERGINI & SARACENO METHOD FOR DIAGONALIZING QUANTUM BILLARDS

A little-known and little-appreciated solution to the long-standing awkwardness and unreliability of calculating chaotic billiard eigenstates was invented recently (described very briefly in E. Vergini and M. Saraceno, Phys. Rev. E 51, 2204 (1995) ). This method finds the cluster of all states in a classically-small k (wavevector) range (roughly 0.2/R, where R is the maximum billiard radius), so is about 1000 times faster than `sweeping' methods (which search for minima of a singular value or determinant as a function of k - the common Heller's tension method and Boundary Integral Method fall into this category), at typical k of a few hundred. Moreover, the relative efficiency increases linearly with k !

I am working to extend Vergini's analysis of the errors in this method, which arise from 2 causes: 1) the inability of the basis to represent general solutions to the Helmholtz equation at a single k value (without requiring exponentially large coefficients), and 2) the deviation of the dilation matrix M from the identity (M is the matrix studied above). Vergini has made tremendous progress in creating a seemingly asymptotically-complete basis set for the stadium billard - I am working on extending this to more general shapes (using the three components: real plane waves, evanescent plane waves, and Neumann-type Bessel functions), with Natasha Lepore. The deviation of M from identity is responsible for the sixth-power growth of tension errors, also found by Vergini, however, how this power-law arises is under investigation.

vector electromagnetic calculation of dielectric waveguide bound modesATOMIC TRAPS AND GUIDES USING DIELECTRIC OPTICAL WAVEGUIDES

I was principal author of a complete proposal for a dipole-force substrate-based trap for neutral atoms. See the paper (156kb .ps.gz) (to appear in Phys. Rev. A 61 Issue 2 (February 2000)). Or download my earlier poster session (350kb .ps) aimed towards the proposed Center for Ultracold Atoms (Harvard / MIT / Wellesley).

In brief, I implemented a non-uniform finite element solution for the full vector bound modes of a submicron dielectric optical waveguide, to assess its potential as an evanescent-field atom trap. For simplicity a rectangular guide was chosen, and the optimal trap design was found in the parameter space of height and width, under the constraint that the guide remain optically `single-mode' (ie one vertically and one horizontally polarized bound mode). By feeding red- and blue-detuned light down the guide with these 2 orthogonal polarizations, a stable potential minimum is felt by the atoms, due to the near-resonant dipole force. Trapped in the xy plane, they are free to travel in the z axis, and the device can operate in both incoherent and coherent regimes.

This work was chiefly in conjunction with Steve Smith (now at Draper Labs), Maxim Olshanii (now at USC), and Mara Prentiss of the Prentiss Group.

I have also worked on a new refractive index structure for high-power single-mode erbium-doped fiber laser designs which allow large mode area, with Mara Prentiss. This requires creating refractive-index profiles that allow stable propagation of modes very close to optical cutoff - two conflicting requirements.

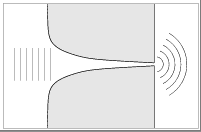Schematic of asymmetric QPC systemQUANTUM POINT CONTACT MAXIMUM CONDUCTANCE, CROSS SECTION AND SCATTERING IN THE HALF-PLANE

I model conductance through a general 2DEG constriction (`Quantum Point Contact'), for instance in the presence of a nearby curved resonator "mirror" (a structure under study in the experiments of the Westervelt group here at Harvard). The existence of such a resonator allows the conductance to reach a single conductance quantum (e^2/h per spin) through an arbitrarily small hole! If many resonances overlap, the conductance can theoretically exceed this (unlikely to be experimentally observed, since the resonances are extremely narrow). Based on the continual stream of ideas from Rick Heller, and with early input on 2D scattering theory from Adam Lupu-Sax, I developed an alternative to the `lead' and `reservoir' picture (Landauer formula for the relation of conductance to transmission matrix elements between `lead' states), which involves scattering cross section in the infinite half-plane. Conductance is equal to the angular integral of the transmission cross section, divided by the de Broglie wavelength. The requirement of a thermal occupation of incoming waves for conductance quantization emerges naturally.

A new radial basis set of partial-wave type states in the half-plane is appropriate to problems where usual `leads' cannot be defined (eg there are nearby scattering objects in the reservoirs, or the QPC is highly non-adiabatic). I develop this basis, and show it behaves just like usual transverse lead states as far as Landauer is concerned. It is also possible to express incident plane-waves in this basis, making connection with the cross section viewpoint. Furthermore, it furnishes scattering-theorists' analogies: a small hole in a wall is shown to be dominated by p-wave scattering and transmission. The p-wave transmission coefficient is found analytically using matching to the Laplace (k=0) solution local to the hole.

`Conductance' quantization of atom waves through a QPC has been recently proposed as an experiment by Joseph Thywissen of the Prentiss Group (now moving to Paris). I show that reciprocity of conductance (left-to-right = right-to-left) need not hold in such an atomic system, because there need not be a thermal occupation of incoming waves (the angular distribution may not be uniform).

This work is in conjuction with Miriam Blaauboer and Areez Mody. Download our paper.
 


Head for advisorland and theHeller Group home page...