V63.0394 Mathematical Wave Dynamics: SPRING 2004

Oliver Buhler and Alex Barnett

colliding NLSE solitons (Valdman)

cavity resonances (Bober)

JUMP TO...

Lecture notes

Problem sets

Resources

Final reports & code

CIMS VIGRE program

Download: Course flyer, and Syllabus. Notice that our assigned room is now 1314 Warren Weaver Hall.

Waves and wave propagation are ubiquitous in nature and lead to many puzzling questions. For instance, what produces mirages in the desert? Why is it that a storm over the ocean sets off a steady swell of small-amplitude waves, but an earthquake at the sea floor can release an enormous flood wave? Can you hear the shape of a drum? In response to these questions, a great deal of mathematics has been developed to understand and predict the dynamics of light or sound waves, the propagation of quantum (matter) waves, the vibration patterns of elastic bodies, or the peculiar nature of water waves. This course will give a guided tour of mathematical wave theory together with physical applications, including normal mode theory, the linear wave equation, superposition, interference and diffraction, short-wavelength asymptotics and ray theory, dispersion, and nonlinear waves and solitons. By the last few weeks of the course, each student will have chosen a topic for more intensive study, and will work towards a final oral presentation and written report. Typically this will involve numerical investigation on a computer (in which case programming experience is helpful), but a theoretical topic is also possible.

This new course is part of the Courant's VIGRE program, and uses the `undergraduate mathematics laboratory' concept of bringing advanced undergraduates together with postdocs and professors to work on current pure or applied research topics, usually with computer experiments.


Lecture theory summary notes, weekly schedule:

  1. Simple harmonic motion and normal modes and applet which demonstrates this (slow the simulation speed way down and go to 2 masses).
  2. Variational method, continuous wave equation, Fourier modes, and applet for playing with the wave equation (string under tension).
  3. Traveling solutions, reflection, energy, plane waves, material interface
  4. WKB, 2D wave equation and plane waves, 2D refraction, Matlab code for today's WKB plot. (Kac drum problem links are below).
  5. Dispersion and ray method, Hamilton's equations, applets illustrating dispersion (Schrodinger equation): 1d quantum mechanics and another.
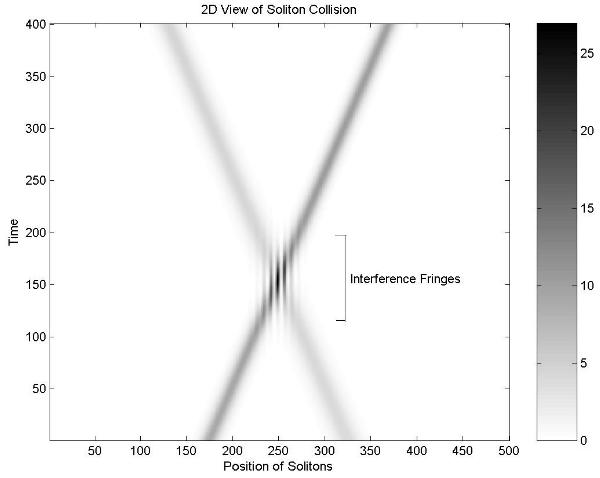
  6. Nonlinear waves, traffic flow, shocks, solitons, Burger's applet and links on shocks and this amazing supersonic flyby, and solitons.
  7. Presentation of available student projects.
  8. Finite Difference methods for the time-dependent Schrodinger equation, see R. LeVeque notes Ch. 1, 2.4, 6.2, Numerical Recipes Ch. 19.0, 19.4 (both linked below).
  9. Up-winding FD schemes and finite volume techniques for 1-way wave equation (advection & traffic flow). matlab code for O(dx) Godunov method.
  10. Radiating systems and the Greens function. In-class project work.
  11. April 6: Preliminary student presentations (10 minutes each).
  12. Assessing convergence of a numerical scheme. In-class project work.
  13. More in-class project work.
  14. April 27th: Final Presentations (20 minutes each). Final written reports due 2pm May 4th! For ideas on typesetting your report, and giving a scientific talk, see Other resources below.

Problem set related:

  1. Matlab code solution for problem set #1.
  2. Problem Set #2, due Feb 17, 2004. Matlab code to generate solutions.

RESOURCES

Wave theory resources and demonstrations:

Numerical resources:

MATLAB resources:

Other resources:

PROJECTS

Initial topic ideas

Mid-semester project choice: download list (as of week 7).

Final student reports