


Next: Applying boundary conditions and
Up: Appendix I: Scaling expansion
Previous: Expansion of the dilation
Curvilinear boundary coordinates
We express 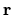 for
for 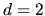 in the form
in the form 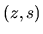 where
where
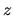 is the outward normal coordinate, and
is the outward normal coordinate, and
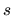 is a (periodic)
tangential location on the boundary
is a (periodic)
tangential location on the boundary 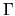 , increasing in an anti-clockwise
fashion
(see Fig. I.1).
I will assume
, increasing in an anti-clockwise
fashion
(see Fig. I.1).
I will assume 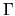 is a curve differentiable to sufficient order.
The corresponding locally-orthonormal unit vectors are
is a curve differentiable to sufficient order.
The corresponding locally-orthonormal unit vectors are 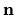 (normal)
and
(normal)
and 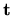 (tangential).
In our curvilinear coordinates they are vector fields defined
by
(tangential).
In our curvilinear coordinates they are vector fields defined
by
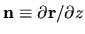 and
and
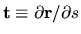 .
For an introduction to such noncartesian systems see [7].
For the local components of the gradient of a scalar field
I will use the abbreviations
.
For an introduction to such noncartesian systems see [7].
For the local components of the gradient of a scalar field
I will use the abbreviations
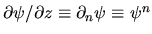 in the normal direction, and
in the normal direction, and
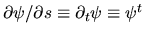 in the tangential direction.
A general vector field
in the tangential direction.
A general vector field 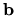 will have the components
will have the components 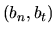 with
with
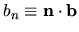 and
and
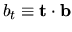 .
.
Our task is to express (I.2) in terms of 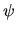 ,
, 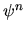 ,
,
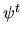 , and higher derivatives
, and higher derivatives 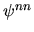 ,
, 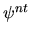 etc.
We will choose a point
etc.
We will choose a point
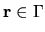 , so that these derivatives
are evaluated at the boundary.
The boundary conditions will later be applied.
We need rules for handling derivatives.
The metric is such that derivatives of the unit vectors obey
, so that these derivatives
are evaluated at the boundary.
The boundary conditions will later be applied.
We need rules for handling derivatives.
The metric is such that derivatives of the unit vectors obey
on the boundary (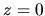 ).
The local inverse radius of curvature of the boundary is
).
The local inverse radius of curvature of the boundary is
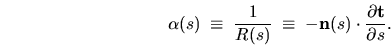 |
(I.5) |
Thus 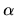 gives the `connection' of the metric (or Christoffel symbol
[7]).
This means that while derivatives of scalars obey the usual Cartesian rules,
derivatives of vectors (or their local components) introduce extra terms.
This key observation was omitted in the work of VS [195,194].
For a general vector field
gives the `connection' of the metric (or Christoffel symbol
[7]).
This means that while derivatives of scalars obey the usual Cartesian rules,
derivatives of vectors (or their local components) introduce extra terms.
This key observation was omitted in the work of VS [195,194].
For a general vector field 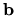 we have,
we have,
The four derivative terms on the RHS are the components of the
covariant derivative tensor.
If we apply the above to the choice
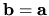 which we take to be a constant
(translation) field according to the prescription of the previous section,
then all the derivatives of
which we take to be a constant
(translation) field according to the prescription of the previous section,
then all the derivatives of 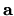 vanish leaving
vanish leaving
which we will use later.
We will also need the divergence of a general
vector field 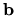 , which is not
simply
, which is not
simply
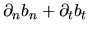 , but rather
, but rather
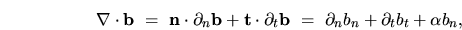 |
(I.13) |
the trace of the covariant derivative tensor.
Choosing
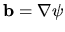 finally gives the Laplacian
finally gives the Laplacian
 |
(I.14) |
equivalent to the form in locally-cylindrical coordinates.



Next: Applying boundary conditions and
Up: Appendix I: Scaling expansion
Previous: Expansion of the dilation
Alex Barnett
2001-10-03
![]() for
for ![]() in the form
in the form ![]() where
where
![]() is the outward normal coordinate, and
is the outward normal coordinate, and
![]() is a (periodic)
tangential location on the boundary
is a (periodic)
tangential location on the boundary ![]() , increasing in an anti-clockwise
fashion
(see Fig. I.1).
I will assume
, increasing in an anti-clockwise
fashion
(see Fig. I.1).
I will assume ![]() is a curve differentiable to sufficient order.
The corresponding locally-orthonormal unit vectors are
is a curve differentiable to sufficient order.
The corresponding locally-orthonormal unit vectors are ![]() (normal)
and
(normal)
and ![]() (tangential).
In our curvilinear coordinates they are vector fields defined
by
(tangential).
In our curvilinear coordinates they are vector fields defined
by
![]() and
and
![]() .
For an introduction to such noncartesian systems see [7].
For the local components of the gradient of a scalar field
I will use the abbreviations
.
For an introduction to such noncartesian systems see [7].
For the local components of the gradient of a scalar field
I will use the abbreviations
![]() in the normal direction, and
in the normal direction, and
![]() in the tangential direction.
A general vector field
in the tangential direction.
A general vector field ![]() will have the components
will have the components ![]() with
with
![]() and
and
![]() .
.
![]() ,
, ![]() ,
,
![]() , and higher derivatives
, and higher derivatives ![]() ,
, ![]() etc.
We will choose a point
etc.
We will choose a point
![]() , so that these derivatives
are evaluated at the boundary.
The boundary conditions will later be applied.
We need rules for handling derivatives.
The metric is such that derivatives of the unit vectors obey
, so that these derivatives
are evaluated at the boundary.
The boundary conditions will later be applied.
We need rules for handling derivatives.
The metric is such that derivatives of the unit vectors obey