The quantity of interest is the matrix of overlaps
![]() .
The eigenstates
.
The eigenstates ![]() are dependent on the deformation parameter
are dependent on the deformation parameter ![]() .
The overlap is taken in position-space
.
The overlap is taken in position-space ![]() over the domain
over the domain
![]() , defined as the intersection
of the undeformed domain
, defined as the intersection
of the undeformed domain
![]() and the deformed domain
and the deformed domain
![]() .
We seek a way to perform these
.
We seek a way to perform these ![]() -dimensional domain integrals rapidly
(in our case
-dimensional domain integrals rapidly
(in our case ![]() ).
Appendix H shows that because the eigenvalues
).
Appendix H shows that because the eigenvalues ![]() and
and
![]() are (in general) different, there exists a very simple formula
(H.5)
for computing this integral using only the boundary.
This will be a huge saving in effort.
are (in general) different, there exists a very simple formula
(H.5)
for computing this integral using only the boundary.
This will be a huge saving in effort.
Because our eigenstates have Dirichlet boundary conditions, a simplification
can be made. Define ![]() (
(![]() ) as the part of
) as the part of ![]() (
(![]() ) inside
) inside
![]() (
(
![]() ).
Then
).
Then
![]() , where
, where ![]() is the boundary of the
intersection region
is the boundary of the
intersection region ![]() .
Then the overlap integral over
.
Then the overlap integral over ![]() can be written
can be written
Given the overlap matrix ![]() at each
at each ![]() , its average profile was found by
the smoothing method of Section C.2.
The smoothing width
, its average profile was found by
the smoothing method of Section C.2.
The smoothing width ![]() was chosen to be 0.02 in wavenumber units,
which was a couple of times the mean level spacing
was chosen to be 0.02 in wavenumber units,
which was a couple of times the mean level spacing
![]() .
.
The resulting sequences of profiles are shown in Fig. 6.14
and 6.15.
Comparison with the first-order perturbation theory (FOPT) result,
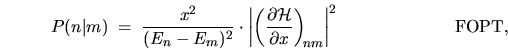 |
(6.31) |