I am a Senior Research Scientist in the
Center for Computational Mathematics (CCM)
at the
Flatiron Institute.
I am also part of a much larger research effort in the area of
machine learning.
I work broadly across the areas of high dimensional data analysis, latent variable modeling, variational inference, deep learning, optimization, and kernel methods. Within CCM, I am attempting to build a group with diverse backgrounds and interests. Currently we have job openings for summer interns, three-year postdocs, and
full-time research scientists (at all levels of seniority).
Before joining Flatiron, I was a tenured faculty member at
UC San Diego and UPenn and a member of the technical staff at
AT&T Labs.
I also served previously as Editor-in-Chief of JMLR and as program chair for
NeurIPS.
I obtained my PhD in Physics from MIT, with a thesis on exact computational methods in
the statistical mechanics of disordered systems.
Recent Projects
High dimensional data analysis
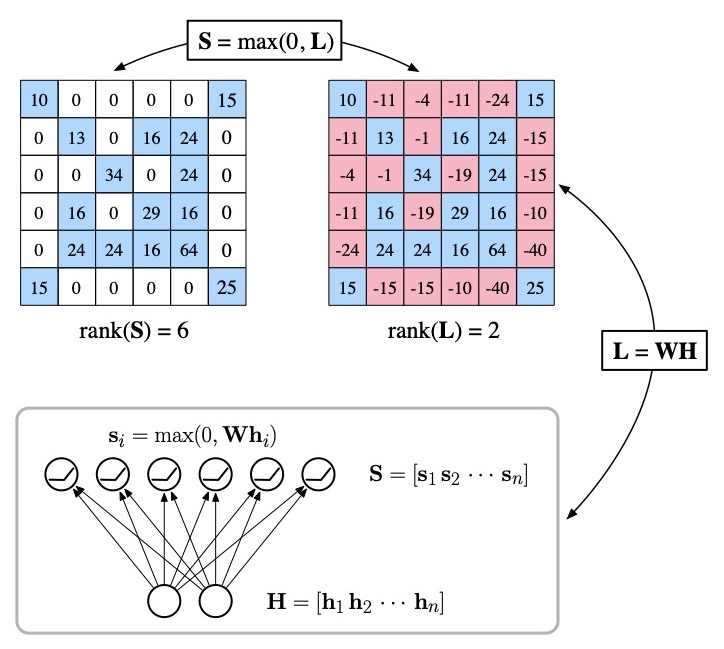
Sparse matrices are not generally low rank, and low-rank matrices are not generally sparse. But can one find more subtle connections between these different properties of matrices by looking beyond the canonical decompositions of linear algebra? This paper describes a nonlinear matrix decomposition that can be used to express a sparse nonnegative matrix in terms of a real-valued matrix of significantly lower rank. Arguably the most popular matrix decompositions in machine learning are those—such as principal component analysis, or nonnegative matrix factorization—that have a simple geometric interpretation. This paper gives such an interpretation for these nonlinear decompositions, one that arises naturally in the problem of manifold
learning.
Learning with symmetries
Gradient descent is based on discretizing a continuous-time flow, typically one that descends in a regularized loss function. But what if for all but the simplest types of regularizers we have been discretizing the wrong flow? This paper makes two contributions to our understanding of deep learning in feedforward networks with homogeneous activations functions (e.g., ReLU) and rescaling symmetries. The first is to describe a simple procedure for balancing the weights in these networks without changing the end-to-end functions that they compute. The second is to derive a continuous-time dynamics that preserves this balance while descending in the network's loss function. These dynamics reduce to an ordinary gradient flow for l2-norm regularization, but not otherwise. Put another way, this analysis suggests a canonical pairing of alternative flows and regularizers.
