Chapter 7: Quantum point contact conductance and scattering in the half-plane

This third part continues the theme of wave mechanics of non-interacting particles. However attention shifts from closed to open systems, namely the transport of quasiparticles (in a 2D electron gas) though a general two-terminal mesoscopic electronic device, or `quantum point contact' (QPC) [20,65].

We model the conductance of a QPC, in linear response. If the QPC is highly non-adiabatic or near to scatterers in the open reservoir regions, then the usual distinction between `leads' and `reservoirs' breaks down. This situation arises in the recent experimental work of Katine [112] and Topinka [192] in the Westervelt group here at Harvard, where open resonant and scattering geometries were studied. In such systems the Landauer formula [129,130,41,55,65] for the conductance (including spin degeneracy),

$$G \; = \; \frac{2e^2}{h} \mbox{Tr}( t^\dag t) ,$$ (1.6)

is no longer convenient because no conventional transverse `lead' states exist between which to define the transmission matrix $t$. Rather, a technique based on scattering theory in the two-dimensional infinite half-plane is appropriate. We relate conductance to transmission cross section, defined as an effective collision size on the reflective boundary of a half-plane (reservoir) region. We also introduce a new half-plane radial basis of `lead' states in which the usual Landauer formula is recovered.

The relation between the Landauer and the half-plane scattering formalism is expressed by

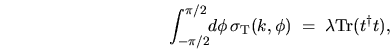$$\int_{-\pi/2}^{\pi/2} \!\! d\phi \, \sigma_{\rm T}(k,\phi) \; = \; \lambda \mbox{Tr} (t^\dag t),$$ (1.7)

where $\sigma_{\rm T}(k,\phi)$ is the angle-dependent transmission cross section and $\lambda$ the Fermi wavelength, which I derive for both hard-walled and soft-walled reflective potential barriers.

We analyse an idealized, highly non-adiabatic slit QPC system in the extreme quantum, intermediate, and semiclassical regimes. We derive the counterintuitive result (first due to Heller) that an arbitrarily small (tunneling) QPC can reach a p-wave channel conductance of $2e^2/h$ when coupled to a suitable resonant cavity. We also find that if two or more resonances coincide, the total conductance can in theory reach multiples of this value.

This leads to some thought-experiments on attempting to overcome the maximum conductance $2e^2/h$ per quantum channel. We also discuss reciprocity (left-to-right symmetry) of conductance, and the possibility of its breakdown in a proposed QPC (which could exhibit `conductance' quantization) for atom waves[191]. We emphasizes the importance of the thermal occupation of states in phase space (as is usual in 2D electron systems), for reciprocity to exist. An analogous atomic QPC in 3D need not have this thermal occupation, thus in this system reciprocity can be broken.

This work has been in collaboration with Areez Mody and Miriam Blaauboer, and at the earlier stages many contributions were made by Adam Lupu-Sax. Joseph Thywissen, and professors Charlie Marcus and Daniel Fisher also contributed via stimulating discussions.