Chapter 7: Conductance of quantum point contacts and half-plane scattering

The quantum point contact (QPC)[20,65] has played a central role in the understanding of mesoscopic conductance. It is the simplest example of a 2DEG system where the quantum coherent nature of the electron controls the bulk transport properties. The Landauer-Büttiker (LB) formalism [129,130,41,55,65] reduces the calculation of quantum conductance in the linear response regime to the evaluation of single-particle wavefunction transmission amplitudes. Traditionally, these amplitudes are measured between travelling wave basis states in the `leads'. Far from the scattering system the leads have constant profiles of finite-width, and support a finite number of transverse modes (channels). Eventually the leads are impedance-matched (that is, without reflection) into `reservoirs' which act as thermalized sources of electrons at their respective potentials; these potentials are taken to reflect the measured bias voltage (hence the resulting conductance is between points deep within the reservoirs). Such theoretical constructs have been remarkably successful at describing transport phenomena, for instance conductance quantization [193,20,65], because the scattering systems involved have generally had good lead-to-reservoir matching.

We consider `open' 2-terminal mesoscopic systems, namely those where a QPC is non-adiabatic (possessing rapid longitudinal variation in transverse profile<sup>7.1</sup> [20]) and has short or nonexistent leads (for instance if it suddenly abutts onto the `reservoir' regions), or those where there can be scattering off nearby objects in the `reservoir' region. We call such systems `open' because the fully two-dimensional (2D) nature of the `reservoirs' (i.e. the surrounding semi-infinite regions of free space) is important, and therefore they cannot be reduced using the quasi-1D approach described above. This includes a variety of recent mesoscopic experiments, for example the combination of QPCs with nearby resonator structures [112] or with a nearby depletion region underneath an AFM tip [192]. It also includes any QPC system where elastic backscattering from disorder in the reservoirs is significant, or generally where the lead-reservoir matching is bad. In such systems, the conventional quasi-1D picture does not apply: the scattering system is not coupled to leads in the usual sense, indeed the distinction between leads and reservoirs is no longer clear. (The quasi-1D approach can be retained by attaching very wide leads to such systems, following [189], although this has both numerical and conceptual limitations). The aim of the present work is to introduce a 2D scattering approach which can handle such systems, and to consider some of the consequences for mesoscopic quantum conductance. We will stay within the non-interacting quasiparticle picture, consider zero applied magnetic field, and assume spin degeneracy of 2 throughout.

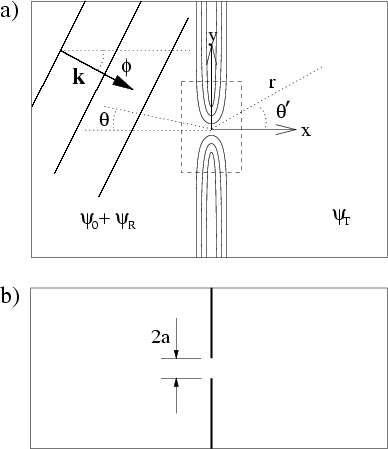
We imagine a geometry where a 2DEG exists in two semi-infinite half-plane regions, separated by an impenetrable potential barrier which we align with the $y$-axis (see Fig. 7.1a). Our general `QPC scattering system' is any gap in this barrier which allows coupling of the wavefunction on the left and right sides. This gap can be defined by an arbitrary form of the elastic potential, and may include other nearby scattering objects, disorder, etc. (which would all be placed within the box shown in Fig. 7.1a). The only important limitation is that this coupling region (the `system') be of finite $y$ extent, so that electrons which leave the system do so via a well-defined terminal: either the left ($x<0$) or the right ($x>0$). We also assume that the system size $L$ is much smaller than both the dephasing length $l_\phi$ and the momentum relaxation (elastic scattering) length $l_e$. The former requirement allows treatment using a coherent wavefunction across the system; the latter allows free-space elastic scattering concepts to be applied.

The conventional distinction between `reservoir' and `lead' is no longer applicable, however at short distances outside the system ($r > L$ but $r \ll l_\phi$ and $r \ll l_e$) the two semi-infinite free space regions behave like leads, since they support scattering-free `channels' (see Section 7.2). At large distances the same regions behave as reservoirs: for $r \gg l_e$ ergodicity ensures that the momentum distribution is uniform in angle, and for $r \gg l_\phi$ the energy is redistributed to ensure equilibrium at the relevant (experimentally-measured) chemical potential of each terminal. In the intermediate region, there is a broad cross-over from lead to reservoir.

In this work we first derive a general relation between transmission cross section (a concept we define using scattering in the half-plane) and conductance for this open geometry, in Section 7.1. In Section 7.2 we show that partial-wave type states, defined in the half-plane regions, can take the place of transverse lead modes in the Landauer formula. In Section 7.3 we examine an idealized, highly non-adiabatic QPC (a hole in a thin hard wall), for which we discuss the small hole (tunneling), large hole (semiclassical) and intermediate regimes. In Section 7.4 we discuss the maximum conductance through this QPC, which is reached when a resonator is placed on one side of the QPC. We find a universal result regardless how small the hole is. This illuminates the findings of a recent experiment[112] in such an open geometry. In Section 7.5 we discuss attempts to exceed the universal quantum of conductance in a single channel. A reciprocity relation for cross section is derived in Section 7.6, and the possibility of breaking this reciprocity, due to a non-thermal reservoir occupation, is described. We discuss an application to matter-wave `conductance' through a 3D QPC. Finally we conclude in Section 7.7.

Figure 7.1: Schematic QPC geometry in 2D: a) general point contact scatterer coupling two semi-infinite regions of free space. The solid curves are contours of an elastic scattering potential $V{({\mathbf r})}$. The `system' size $L$ (dashed box) we take to be the region where $V{({\mathbf r})}$ has not yet reached its asympotic form (which is zero apart from a $y$-invariant profile around the $y$-axis). Also shown are an incoming plane wave, and the coordinate system. b) The idealized `slit' aperture in a thin, hard wall considered in Section 7.3.