- ...
linearly1.1
- The relation depends upon the initial energy distribution.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
grasp1.2
- Some idea
of the rate of progress of this technology can be gained from such quotes as
``Such a machine in the hands of a competent operator can produce 400 full-length
products or 1,000 sums during an 8-hour working day''[42],
referring to an electromechanical desk calculator typical for scientific use in
the 1950s.
The diagonalization of an 8-by-8 matrix was a weekend-long task[125].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... profile2.1
-
Note that I will also refer to
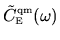 as the band profile, since it
differs only by a constant factor.
as the band profile, since it
differs only by a constant factor.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... formula3.1
-
This formula was first found (in
 ) by Wallace Clement
Sabine in 1898, in his studies of Harvard's own
Jefferson Laboratory main
auditorium, room 250.
Sabine used
this expression for the mean free path to give a formula for the
reverberation time of a hall [21,173].
) by Wallace Clement
Sabine in 1898, in his studies of Harvard's own
Jefferson Laboratory main
auditorium, room 250.
Sabine used
this expression for the mean free path to give a formula for the
reverberation time of a hall [21,173].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... vector3.2
-
The cross-product form used here for
 and
and
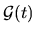 is strictly valid in 2D and 3D only.
For
is strictly valid in 2D and 3D only.
For 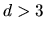 the higher-dimensional generalization of a
general rotation should
be used.
the higher-dimensional generalization of a
general rotation should
be used.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... components4.1
-
The condition that a deformation
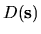 not move the `center
of mass' (centroid
of the cavity volume) is
not move the `center
of mass' (centroid
of the cavity volume) is
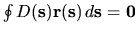 .
This is in general different from the condition for
having zero overlap with translations, namely
.
This is in general different from the condition for
having zero overlap with translations, namely
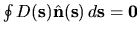 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Vergini 6.1
-
Personal communication.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... volume6.2
- For an example of appearance of surface
waves in an example
problem in linear spaces see [77].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... state6.3
- as also found by E. Vergini, personal communication.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... do6.4
- This is an elaboration of a suggestion
of Vergini (personal communication).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... profile7.1
-
By non-adiabatic, we mean that even at a QPC's narrowest region
the transverse profile is changing rapidly.
Clearly every QPC becomes `non-adiabatic' at the coupling to
infinite-width reservoirs:
this type of non-adiabaticity we do not include because it
does not cause significant impedance mismatch, as explained in
Ref. [206].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... region7.2
-
Of course, throughout this chapter
we could imagine the incident wave on the right-hand side,
and the same conductance would result (since we are in linear
response); see Section 7.6.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... profile7.3
-
We could equally well
imagine that the QPC can be `closed off'
(no transmission) by varying a parameter
(this is often true experimentally), and define
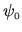 as the full wavefunction in this closed-off state.
Thus
as the full wavefunction in this closed-off state.
Thus
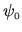 would be the sum of an incident plane wave
and a more complicated outgoing wave.
This alternative definition may be better in
systems where the wall has disorder, or where there is more
complicated structure
on the left-hand side than shown in Fig. 7.1a.
The two definitions are equivalent as far as Sections 7.3 and
7.4 are concerned.
would be the sum of an incident plane wave
and a more complicated outgoing wave.
This alternative definition may be better in
systems where the wall has disorder, or where there is more
complicated structure
on the left-hand side than shown in Fig. 7.1a.
The two definitions are equivalent as far as Sections 7.3 and
7.4 are concerned.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...sakurai)
7.4
-
Presentations of two-dimensional scattering theory are rare;
see [132,3,43].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... wall7.5
-
This argument can also be verified in the more specific case
of the left region being a
rectangular Dirichlet box, in which case the exact eigenfunctions
are known and can be written explicitly in terms of a sum of
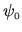 for incidences
for incidences 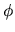 and
and 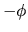 .
However the phase-space presentation is more general, and applies
to the real situation where the left region is chaotic (diffusive
elastic scattering).
.
However the phase-space presentation is more general, and applies
to the real situation where the left region is chaotic (diffusive
elastic scattering).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... regime7.6
-
The only requirement for this 1D argument to hold is that the
effective longitudinal potential tend to a constant asymptotically.
This allows a 1D density of states to be defined.
It precludes for instance the Mathieu basis mentioned in
Section 7.3, unless a reparametrization of the `radial'
coordinate is performed.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... imply7.7
-
With
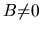 , the conductance is still
symmetric under swapping the leads.
This results from the 2-terminal special case of
unitarity sum rules[55], namely that
the rows and columns of the matrix of absolute-value-squared
, the conductance is still
symmetric under swapping the leads.
This results from the 2-terminal special case of
unitarity sum rules[55], namely that
the rows and columns of the matrix of absolute-value-squared 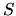 -matrix elements
must all sum to 1.
Thus the reciprocity derived here is preserved for
-matrix elements
must all sum to 1.
Thus the reciprocity derived here is preserved for 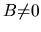 .
How the classical argument from the previous paragraph generalizes for
.
How the classical argument from the previous paragraph generalizes for
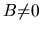 is not known by the authors.
is not known by the authors.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... beam7.8
-
Because we wish to consider general illumination and general
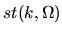 ,
our definition of `conductance' coincides with that of Ref. [191]
only in the case of isotropic illumination
,
our definition of `conductance' coincides with that of Ref. [191]
only in the case of isotropic illumination
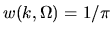 .
The beam brightness per unit
.
The beam brightness per unit 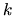 range, that is, its
phase-space density, is assumed uniform in position space,
and is proportional to
range, that is, its
phase-space density, is assumed uniform in position space,
and is proportional to
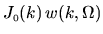 .
This is also proportional to
.
This is also proportional to
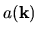 defined in Ref. [191].
defined in Ref. [191].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... defined8.1
- Our definitions
of
 and
and 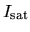 correspond to those of
C. S. Adams et al. [2]
correspond to those of
C. S. Adams et al. [2]
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... frequency8.2
- Even though
the frequencies will actually
differ
by a couple of percent because of
their detunings, and cause a difference in decay lengths of the correct sign,
this effect alone is not large enough to create large
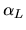 values. Future designs with larger detunings, possibly much larger
than the fine splitting,
may be able to
use this effect alone
values. Future designs with larger detunings, possibly much larger
than the fine splitting,
may be able to
use this effect alone
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... direction8.3
- Following
the notation of Fernandez &
Lu[139] for rectangular guides,
mode
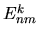 has
has 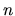 (
(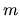 ) antinodes in the
) antinodes in the 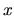 (
(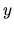 ) direction,
and overall polarization axis
) direction,
and overall polarization axis 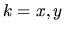 .
However as the symmetry line
.
However as the symmetry line 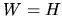 is approached
(see Figure 8.2),
mixing of polarizations occurs for the case
is approached
(see Figure 8.2),
mixing of polarizations occurs for the case 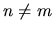 and the notation becomes more arbitrary.
and the notation becomes more arbitrary.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... constant8.4
- We made
the assumption that the positive and negative
detunings caused negligible shifts in the wavelength used for
the bound mode calculation. For the
largest detunings used in this chapter the fractional
shift is 1.8%.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... workstation8.5
-
Silicon Graphics 75MHz R8000
processor commercial compilers, with a
SPEC FP95 rating [186] of between 10 and 12.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
estimated8.6
- For some of the earliest
bending loss estimation in a rectangular fiber see
[142] and for the case of a cylindrical fiber
see [143].
Most of the work done since then has been on
the more complicated situation of fibers with cladding.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... complicatedA.1
- Doron Cohen,
personal communication.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... belowD.1
-
I have found other examples, for instance the deformation field
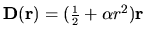 is special for the
potential
is special for the
potential
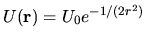 . Such a deformation is dilation-like,
but not a linear dilation given by the symmetric part of
. Such a deformation is dilation-like,
but not a linear dilation given by the symmetric part of 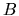 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... sequenceH.1
-
This will not be given, but briefly it involves expanding the second term,
use of Gauss' theorem and the identity
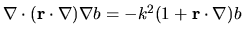 .
Meanwhile the first term is compared to the volume integral of
.
Meanwhile the first term is compared to the volume integral of
![$\nabla\cdot[\nabla a^*({\mathbf r}\cdot\nabla b)]$](img1816.gif) and its expansion, using
the identity
and its expansion, using
the identity
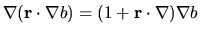 .
Both these identities require Einstein summation notation to prove.
Bypassing such a tricky maze of formulae is one purpose of this appendix.
.
Both these identities require Einstein summation notation to prove.
Bypassing such a tricky maze of formulae is one purpose of this appendix.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.