


Next: Stochastic energy spreading
Up: Review of the linear
Previous: Basis choice, perturbation theory
Generalized force-force correlation and band profile
Here I show a way to express the average transition rates in terms of the
time correlation function
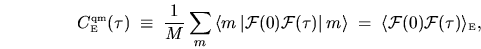 |
(2.46) |
where the (generalized force) operator 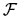 is an abbreviation for
is an abbreviation for
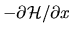 .
Note that
.
Note that
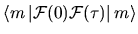 corresponding
to the initial state (2.39)
can be explicitly
written
corresponding
to the initial state (2.39)
can be explicitly
written
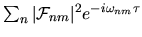 .
Averaging over
.
Averaging over 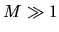 adjacent initial states
adjacent initial states
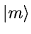 (which nevertheless span a classically-small energy range)
has been performed in order to extract the local average of
the random values of
(which nevertheless span a classically-small energy range)
has been performed in order to extract the local average of
the random values of
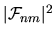 .
This smearing will from now be implied by
the microcanonical ensemble average at energy
.
This smearing will from now be implied by
the microcanonical ensemble average at energy 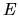 , indicated
by the notation
, indicated
by the notation
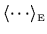 .
The Fourier transform gives the auto-correlation spectrum
.
The Fourier transform gives the auto-correlation spectrum
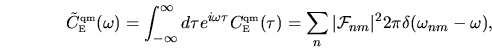 |
(2.47) |
which will play a central role in this
and the following chapters.
Here, as before, the delta function must be taken to have a width
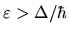 , where
, where 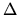 is the mean level spacing in energy.
Thus there are two components to the smoothing (`smearing')
procedure: a smearing by width
is the mean level spacing in energy.
Thus there are two components to the smoothing (`smearing')
procedure: a smearing by width 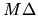 along the diagonal, and
by width
along the diagonal, and
by width
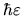 off the diagonal.
The smearing is chosen to be sufficient to allow
off the diagonal.
The smearing is chosen to be sufficient to allow
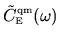 to become a well-defined function of
to become a well-defined function of 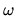 ,
and smooth in
,
and smooth in 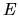 .
By using the continuum limit substitution
.
By using the continuum limit substitution
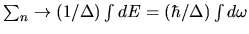 , the auto-correlation spectrum
can now be interpreted as giving a formula for the mean value of the
squared matrix element:
, the auto-correlation spectrum
can now be interpreted as giving a formula for the mean value of the
squared matrix element:
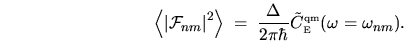 |
(2.48) |
The right-hand side, viewed as a continuous function of 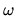 ,
is called the band profile2.1of the matrix
,
is called the band profile2.1of the matrix
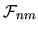 because it measures its off-diagonal (`band') structure.
This construction is illustrated by Fig. 2.3.
The matrix, and hence
because it measures its off-diagonal (`band') structure.
This construction is illustrated by Fig. 2.3.
The matrix, and hence
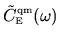 ,
has structure on
,
has structure on 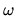 -scales similar to inverse correlation times
of the chaotic motion
(for instance the bouncing rate in a billiard system).
However the dependence on
-scales similar to inverse correlation times
of the chaotic motion
(for instance the bouncing rate in a billiard system).
However the dependence on 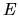 is very much weaker
(if
is very much weaker
(if 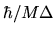 is chosen smaller than the shortest periodic orbit
[200], as discussed in Section 2.3.3),
only changing
over classically-large energy scales, so can be taken as constant in
any classically-small range.
An example matrix from a real system is shown in Fig. 2.7).
is chosen smaller than the shortest periodic orbit
[200], as discussed in Section 2.3.3),
only changing
over classically-large energy scales, so can be taken as constant in
any classically-small range.
An example matrix from a real system is shown in Fig. 2.7).
We can now replace the FGR transition
rate by its well-defined average over the width of the delta-like functions,
![\begin{displaymath}
\langle \Gamma_{nm}(\omega)\rangle \; = \;
\frac{A^2}{4} \...
...[ \delta(\omega_{nm} - \omega) + \delta(\omega_{nm} + \omega)]
\end{displaymath}](img310.gif) |
(2.49) |
which is given by the band profile.



Next: Stochastic energy spreading
Up: Review of the linear
Previous: Basis choice, perturbation theory
Alex Barnett
2001-10-03
![]() , where
, where ![]() is the mean level spacing in energy.
Thus there are two components to the smoothing (`smearing')
procedure: a smearing by width
is the mean level spacing in energy.
Thus there are two components to the smoothing (`smearing')
procedure: a smearing by width ![]() along the diagonal, and
by width
along the diagonal, and
by width
![]() off the diagonal.
The smearing is chosen to be sufficient to allow
off the diagonal.
The smearing is chosen to be sufficient to allow
![]() to become a well-defined function of
to become a well-defined function of ![]() ,
and smooth in
,
and smooth in ![]() .
By using the continuum limit substitution
.
By using the continuum limit substitution
![]() , the auto-correlation spectrum
can now be interpreted as giving a formula for the mean value of the
squared matrix element:
, the auto-correlation spectrum
can now be interpreted as giving a formula for the mean value of the
squared matrix element: