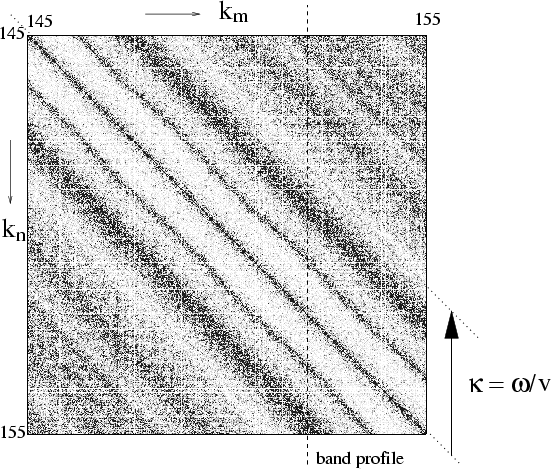
The classical band profile (found using methods in Appendix B)
and quantum band profile (methods in Appendix C)
are compared in Fig. 2.5, for
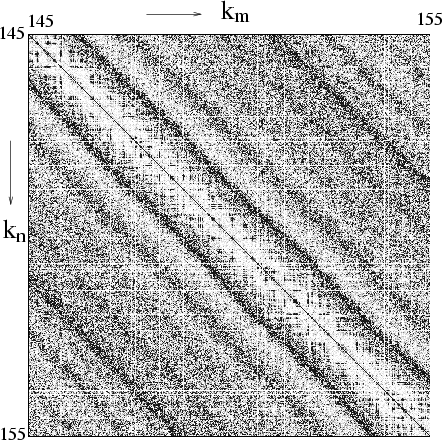
the two-dimensional billiard system shown in Fig. 2.6.
This system was chosen because
efficient diagonalization methods
(see Chapter 6) exist for billiards,
and a good basis set (Appendix J) is already known for this
shape.
The agreement is excellent, well within the expected RMS estimation
errors for all ![]() considered.
Note that there
are no fitted parameters in this comparison.
The three different
choices of the effect of parameter
considered.
Note that there
are no fitted parameters in this comparison.
The three different
choices of the effect of parameter ![]() are different `deformations' of the
billiard (the subject of the following two chapters).
The range of
are different `deformations' of the
billiard (the subject of the following two chapters).
The range of ![]() studied goes from zero to beyond the frequency
of the shortest period orbit (the `bouncing ball' orbit family).
Note that this agreement has also been tested for other
example systems [49,48].
The conclusions can be drawn that
classical correlation functions can give a good semiclassical estimate
of averaged quantum matrix elements, and
QCC in the LRT regime has been tested for (at least some) real chaotic systems.
studied goes from zero to beyond the frequency
of the shortest period orbit (the `bouncing ball' orbit family).
Note that this agreement has also been tested for other
example systems [49,48].
The conclusions can be drawn that
classical correlation functions can give a good semiclassical estimate
of averaged quantum matrix elements, and
QCC in the LRT regime has been tested for (at least some) real chaotic systems.
 |
 |