Our basic task is to create intense evanescent light fields with a potential
minimum sufficiently far
from a dielectric surface to make
the surface interaction potential and heating mechanisms
negligible (discussed in Section 8.5.1).
The main difficulty arises because the evanescent fields have
a typical exponential decay length
![]() ,
so if we are to have a trap of useful
depth, we are restricted to keep it within roughly
,
so if we are to have a trap of useful
depth, we are restricted to keep it within roughly ![]() of the surface
(less than a micron).
of the surface
(less than a micron).
A potential minimum in one dimension can be obtained using a blue (repulsive)
light field of higher intensity at the
dielectric surface than the red (attractive) light field, and ensuring the
decay lengths obey
![]() , giving a potential
of the form
, giving a potential
of the form
If we define a normalized decay length difference
![]() , then
we can give two reasons why increasing
, then
we can give two reasons why increasing ![]() is a vital
design objective.
Firstly, it is easy to show that for small
is a vital
design objective.
Firstly, it is easy to show that for small ![]() the deepest available trap depth (found by optimizing the ratio of surface
intensities
the deepest available trap depth (found by optimizing the ratio of surface
intensities
![]() )
scales as
)
scales as ![]() .
Secondly, a larger
.
Secondly, a larger ![]() is beneficial for trap coherence,
(giving
a smaller spontaneous decay rate
at a given trap depth and detuning), because the sum of the
intensities can be kept lower (see equation (8.5)) for a given
intensity difference (equation (8.4)).
We will quantify this latter connection in Section 8.3.1.
is beneficial for trap coherence,
(giving
a smaller spontaneous decay rate
at a given trap depth and detuning), because the sum of the
intensities can be kept lower (see equation (8.5)) for a given
intensity difference (equation (8.4)).
We will quantify this latter connection in Section 8.3.1.
Our two key differences from the proposal of Ovchinnikov et al. are as follows.
Firstly, we create a non-zero ![]() by using two orthogonally-polarized
bound modes of a dielectric slab guide, which have different evanescent decay
lengths at the same frequency8.2.
This contrasts with Ovchinnikov et al.
who suggest varying the decay lengths
by varying the reflection angles from the inside surface of a glass prism.
Secondly, horizontal confinement is achieved by limiting the width of the
slab guide to approximately
by using two orthogonally-polarized
bound modes of a dielectric slab guide, which have different evanescent decay
lengths at the same frequency8.2.
This contrasts with Ovchinnikov et al.
who suggest varying the decay lengths
by varying the reflection angles from the inside surface of a glass prism.
Secondly, horizontal confinement is achieved by limiting the width of the
slab guide to approximately ![]() (forming what is called a channel guide [117]),
which automatically creates a
maximum in each light intensity field
in the horizontal direction. This results in a tight horizontal confinement
in the atomic potential, of similar size to the vertical confinement, and
is something very hard to achieve in a prism geometry.
(forming what is called a channel guide [117]),
which automatically creates a
maximum in each light intensity field
in the horizontal direction. This results in a tight horizontal confinement
in the atomic potential, of similar size to the vertical confinement, and
is something very hard to achieve in a prism geometry.
A schematic of our design is shown in Figure 8.1a.
The optical guide
height ![]() and width
and width ![]() are kept small enough to guarantee
that
there are exactly two bound modes, differing in
polarization but not in nodal structure
(in optical terminology this is called single-mode):
are kept small enough to guarantee
that
there are exactly two bound modes, differing in
polarization but not in nodal structure
(in optical terminology this is called single-mode):
![]() has an electric field predominantly
in the x direction8.3, and is
to be excited by blue-detuned laser light,
and
has an electric field predominantly
in the x direction8.3, and is
to be excited by blue-detuned laser light,
and ![]() has electric field predominantly in the y direction
and is
to be excited by red-detuned laser light.
We can see
why their vertical decay lengths differ by considering the case of the slab
(i.e. taking the width
has electric field predominantly in the y direction
and is
to be excited by red-detuned laser light.
We can see
why their vertical decay lengths differ by considering the case of the slab
(i.e. taking the width
![]() ), where these
modes are simply the slab TE and TM modes respectively.
For both these slab modes the purely transverse field
obeys the differential equation
), where these
modes are simply the slab TE and TM modes respectively.
For both these slab modes the purely transverse field
obeys the differential equation
 |
No analytic solution exists for the general rectangular guide,
so we used the finite element method discussed in Section 8.4
to solve for the bound mode ![]() values and fields as a
function of guide dimensions.
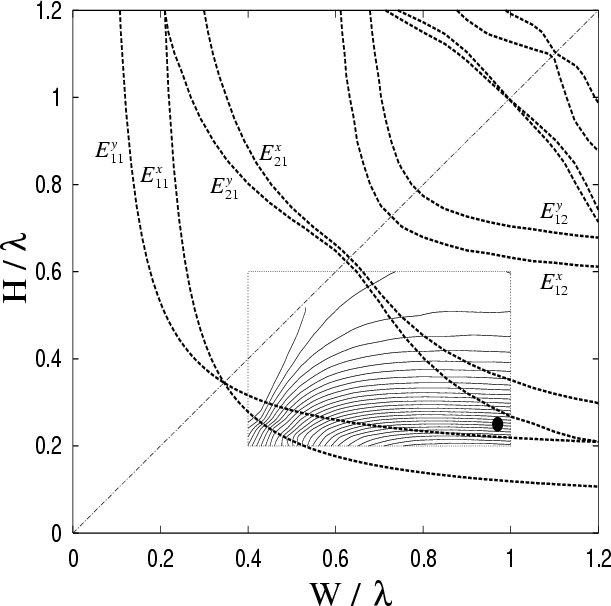
Figure 8.2
shows the resulting `cut-off curves', that is, contours
of constant
values and fields as a
function of guide dimensions.
Figure 8.2
shows the resulting `cut-off curves', that is, contours
of constant ![]() in the parameter space
in the parameter space ![]() .
In this example we chose a guide index
.
In this example we chose a guide index ![]() (typical for a polymer dielectric) and, as a preliminary case,
a substrate index
(typical for a polymer dielectric) and, as a preliminary case,
a substrate index ![]() .
.
The single-mode region, in which we wish to remain,
is bounded below by the ![]() and
and ![]() curves
and above by the
curves
and above by the ![]() curve.
Note that, as in any dielectric guiding structure uniform in the z axis, the
lowest two modes (
curve.
Note that, as in any dielectric guiding structure uniform in the z axis, the
lowest two modes (![]() and
and ![]() in our case)
never truly reach cut-off, rather, they approach it exponentially
as the guide cross-section is shrunk to zero.
For this reason, we chose the practical definition of cut-off for these modes
to be
in our case)
never truly reach cut-off, rather, they approach it exponentially
as the guide cross-section is shrunk to zero.
For this reason, we chose the practical definition of cut-off for these modes
to be
![]() , which corresponds to only about 20% of the power being
carried inside the guide.
In contrast, higher modes do have true cut-offs[183,117]
(this distinction is illustrated
by the dispersion curves of Figure 8.4), and for the
, which corresponds to only about 20% of the power being
carried inside the guide.
In contrast, higher modes do have true cut-offs[183,117]
(this distinction is illustrated
by the dispersion curves of Figure 8.4), and for the ![]() mode our (numerically limited) contour choice of
mode our (numerically limited) contour choice of
![]() falls
very close to the true cut-off curve.
falls
very close to the true cut-off curve.
Using the numerically calculated electric field strengths of the
![]() and
and ![]() modes, we found the red and blue guided laser powers which gave the deepest
trap, subject to the constraint of fixed total power (keeping the
detuning constant 8.4).
We also imposed the restriction that the zero of trapping potential come no
closer than 100nm along the vertical line
modes, we found the red and blue guided laser powers which gave the deepest
trap, subject to the constraint of fixed total power (keeping the
detuning constant 8.4).
We also imposed the restriction that the zero of trapping potential come no
closer than 100nm along the vertical line ![]() , which kept the trap minimum
a reasonable distance from the surface (see Section
8.5.1).
Performing this optimization over a region of the parameter space covering
the single-mode region gave a contour plot of maximum achievable depth for a
given total power, shown within the rectangle overlayed on Figure
8.2.
This depth increases from negligible values in the top left to
the largest depths in the lower right, indicating that choosing
, which kept the trap minimum
a reasonable distance from the surface (see Section
8.5.1).
Performing this optimization over a region of the parameter space covering
the single-mode region gave a contour plot of maximum achievable depth for a
given total power, shown within the rectangle overlayed on Figure
8.2.
This depth increases from negligible values in the top left to
the largest depths in the lower right, indicating that choosing ![]() and
and ![]() to
be in this latter corner of the single-mode region is best for depth.
The depth shows very little variation with
to
be in this latter corner of the single-mode region is best for depth.
The depth shows very little variation with ![]() in this corner, rather
it is clear that varying
in this corner, rather
it is clear that varying ![]() to stay within our definition of
the single-mode region
has become the limiting factor on achievable depth.
We indicate a practical choice of
to stay within our definition of
the single-mode region
has become the limiting factor on achievable depth.
We indicate a practical choice of
![]() and
and
![]() as a small marker on Figure 8.2.
Example trapping potentials shapes possible with these parameters are
shown in Figure
8.3;
we discuss their properties in Section
8.3.
as a small marker on Figure 8.2.
Example trapping potentials shapes possible with these parameters are
shown in Figure
8.3;
we discuss their properties in Section
8.3.
In Figure 8.1a the direct
excitation of the optical guide by the two
laser beams is
shown only schematically.
In a realistic experimental setup this coupling
into the guide would happen on the order of
a centimeter
from the atom guiding region, and could involve tapered or Bragg
couplers[117]
from beams or from other fibers.
At this distance we estimate that isotropic stray
light due to an insertion loss of 0.5
would have 8 orders of magnitude less intensity than
the EW fields in the guiding region.
Assuming the light is coherent, this limits the fractional
modulation of the guiding
potential to ![]() .
More improvements are possible, including the use of absorbing shields,
bending the guide through large angles
away from the original coupling direction, and reducing the coherence length.
.
More improvements are possible, including the use of absorbing shields,
bending the guide through large angles
away from the original coupling direction, and reducing the coherence length.