Introduction

There has been much recent progress in the trapping and cooling of neutral atoms, opening up new areas of ultra-low energy and matter-wave physics [45,51,159]. Waveguides for such atoms are of great interest for atom optics, atom interferometery, and atom lithography. Multimode atom waveguides act as incoherent atom pipes that could trap atoms, transport them along complicated paths or between different environments, or deliver highly localized atom beams to a surface. Single-mode waveguides (or multimode guides populated only by atoms in the transverse ground-state) could be used for coherent atom optics and interferometry [151,2], as well as a tool for one-dimensional physics such as boson-fermion duality [190,152,44] and low-dimensional Bose-Einstein condensation effects [115].

The optical dipole-force has long been used to trap and manipulate atoms [45,51,159] as well as dielectric particles [9,113] (for a review see [10]). The available intensity of lasers has allowed a multitude of such atom traps in the far-detuned regime, giving very low decoherence and heating rates, and storage times on the order of seconds (for a review of dipole-force atom trapping, see [85]).

Evanescent light waves have been popular in many atom mirrors, traps and guides (see the original theoretical work [52,13] and review [67]) since they can provide potentials with high spatial gradients (decay lengths $\sim \lambda / 2 \pi$ where $\lambda$ is the optical wavelength), and use rigid dielectric structures (prisms, fibers) to define the potential shape. For example, there has been a series of repulsive (blue-detuned) evanescent-wave (EW) traps which rely on gravity to provide the counteracting force [4,155] and recent experiments have shown that hollow optical fibers can guide atoms confined within the hollow core using a repulsive evanescent field guided by the fiber [170,102,103].

The idea of using an EW to provide both attractive and repulsive forces is due to Ovchinnikov et al. [156], who proposed the use of two colors (i.e. red and blue detunings) and differing evanescent decay lengths to achieve a trap with the potential minimum a distance $\sim \lambda$ from a prism surface. Until now, this design has been restricted to planar traps (weak confinement in the other two dimensions).

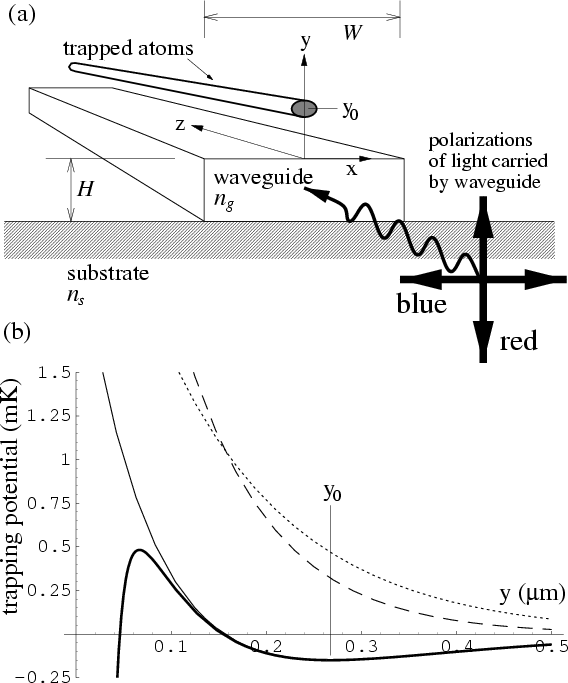
In this chapter we discuss a two-color trap based on the EW fields above a single-mode, submicron optical `channel' waveguide. The trap provides tight confinement in two dimensions and allows free de Broglie wave propagation in the third, forming an atomic waveguide that could transport atoms a between $\lambda/4$ and $\lambda/2$ above the optical guide surface. Our proposal is to utilize the differing vertical evanescent decay lengths of the two polarizations carried in the single-mode optical guide (see Figure 8.1). The physical origin of this decay length difference is the fact that the TM mode is closer to optical cut-off than the TE mode at the same frequency.

Our proposal is reminiscent of some existing resonant enhancement schemes for EW mirrors (demonstrated with surface plasmons [71] and dielectric waveguides [109,124]) but with a radical change from a planar geometry to a linear, the mechanism for exciting the guide, and the simultaneous guiding of a second frequency of opposite detuning. It also shares the feature of two guided colors with an atom trap proposal using microsphere whispering-gallery modes[141].

Our design has many desirable experimental features: 1) very little optical power is required to obtain large trapping intensities since the optical bound mode has very small cross sectional area ( $\sim 0.3 \, \mu m^{2}$), 2) the optical field is non-divergent, so can be maintained over distances orders of magnitude further than diffraction-limited propagation in free space allows, 3) the trapping potential is well-known, mechanically stable, and insensitive to experimental parameters other than the optical powers, since it is defined by single-mode intensity distributions fixed relative to a substrate, 4) fabrication of arrays of closely spaced atom waveguides is possible[176], for parallel lithography or measurement, creating ``on-chip'' integrated atom-optical elements, 5) the atoms are exposed providing additional optical and physical access (a feature not shared with hollow-fiber designs), and 6) the velocity of the atoms along the direction of the waveguide could be controlled by standing waves in the light carried by the optical guide [114].

Compared to a Zeeman-effect magnetic trap for neutral atoms, far-detuned optical dipole-force traps can have comparable trapping times, but typically an order of magnitude less depth and transverse mode spacings than recent magnetic traps [197,97,104,59,190] (for an introduction see [22]). However, in microfabricated applications the stray magnetic fields decay as a power law with distance, whereas evanescent light fields decay exponentially (ignoring for now any scattering into free space caused by optical defects). We believe this could give guided optical traps a distinct advantage in terms of achievable density of independent atom-optical elements on a single substrate.

Also, optical traps have the advantage that there is no significant loss mechanism which can remove atoms from the trap (assuming the thermal energy is much less than the trap depth): spontaneous events cause a small heating rate, and non-adiabatic changes in $m_F$ can change the optical potential but not the fact that the atom remains trapped. This is to be contrasted with a non-adiabatic spin-flip event in a magnetic trap, which results in loss of the atom. This makes optical waveguides particularly attractive for incoherent transport, when the loss of coherence due to the spontaneous events is unimportant. Finally, optical manipulation has the advantage over magnetic manipulation in terms of high possible switching speeds.

This chapter is organized as follows. In Section 8.2 we describe the dipole potential, the exponential approximation for the EW fields, and the mechanism for the difference in decay length. We show how we optimized the optical guide dimensions, in the case of a rectangular guide on a substrate of unity refractive index (for $m_F = 0$), and discuss some design objectives and implementation issues. In Section 8.3 we give simulated results for cesium atoms: trap depth, coherence time, transverse mode spacing and Q factor, and spontaneous heating rate. We also show how depth and coherence time are generally limited by only two parameters (the detuning and the normalized decay length difference). We study both the case of a substrate refractive index of unity, and in Section 8.3.3 the more realistic index of 1.32. We describe the numerical electromagnetic finite element technique in Section 8.4, including the accuracy achieved. Section 8.5 is an investigation of two potential causes of loss or decoherence of atoms, namely interactions with the dielectric surface and bending of the waveguide. Finally in Section 8.6 we conclude and give some future prospects for this proposal.

Figure 8.1: (a) Shows trap geometry, dielectric guide dimensions, incoming laser polarizations, and the cartesian axes; (b) shows the trapping potential above the dielectric along a vertical slice at $x=0$. The component due to red-detuned light (absolute value shown as dotted line) subtracts from that of blue-detuned light (dashed line) to give the total dipole potential $U_{\rm dip}$ (thin solid line). This is modified by the Casimir surface interaction (Section 8.5.1), giving the final potential (thick line). Here the trap depth of 150$\mu$K and coherence time of 12ms is generated in our design by 2 mW total guided laser power detuned by $\pm 15$nm from the cesium D2 line.