


Next: The white noise approximation
Up: The cavity system
Previous: Form of correlation spectrum
Conversion of time averages to averages over collision parameters
This section shows how ergodicity can be
used to go from a time average to a collision
parameter average, for a quantity which takes values at each of the collisions.
This will prove useful for approximating
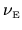 in the next section,
but it can be skipped on first reading.
(It is presented in a more terse form in [46]).
in the next section,
but it can be skipped on first reading.
(It is presented in a more terse form in [46]).
I treat time-averages of quantities which are non-zero only during the
collisions, and whose value during a collision is a function of
the parameters of the collision (angle from the normal, and surface location)
only.
They can be converted to collision-parameter averages, eliminating the
time variable, as follows.
For a hard-walled billiard, imagine a function of phase-space
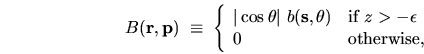 |
(3.6) |
which exists only in the thin shell of thickness 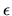 near the wall.
The position vector
near the wall.
The position vector 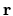 is represented by
is represented by
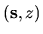 where
where 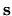 is a surface coordinate and
is a surface coordinate and 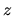 an outward `radial'
coordinate normal to the surface.
an outward `radial'
coordinate normal to the surface.
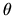 is the angle of the
is the angle of the 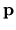 vector from the local normal.
This leaves
vector from the local normal.
This leaves 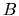 independent of the other
independent of the other 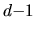 momentum degrees of freedom.
The function
momentum degrees of freedom.
The function
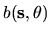 is assumed constant upon reflection,
i.e. it is even about
is assumed constant upon reflection,
i.e. it is even about
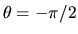 .
The time-dependence of
.
The time-dependence of 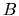 along a given trajectory will be a series of
impulses due to passing through the shell; the duration of impulse
along a given trajectory will be a series of
impulses due to passing through the shell; the duration of impulse 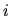 will be
will be
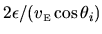 ,
and during this time its value is
,
and during this time its value is
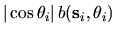 .
Therefore the cos factors cancel, and the time-average is
.
Therefore the cos factors cancel, and the time-average is
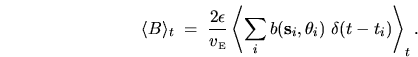 |
(3.7) |
By ergodicity one can equate this to the phase-space average of (3.6)
at the energy 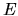 ,
,
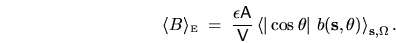 |
(3.8) |
Here I used the fact that in the
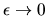 limit
the fraction of position space occupied by the
shell is
limit
the fraction of position space occupied by the
shell is
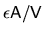 .
This collapses the average to be over
.
This collapses the average to be over 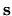 and over the
and over the 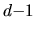 dimensional solid angle
dimensional solid angle 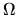 .
Choosing the function
.
Choosing the function 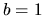 gives a useful expression
for the mean collision rate (the inverse of the ballistic time),
gives a useful expression
for the mean collision rate (the inverse of the ballistic time),
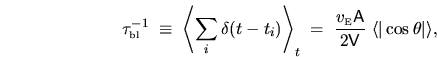 |
(3.9) |
which is a form of Sabine's formula3.1.
The geometrical factor is the solid angle average
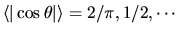 for dimension
for dimension 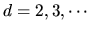 (see Appendix D of [46]).
Or, choosing
(see Appendix D of [46]).
Or, choosing
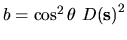 gives
gives
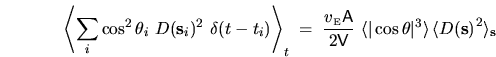 |
(3.10) |
where we used the fact that for this choice
the averages over surface location and solid angle separate.
Again, formulae exist for the
dimension-dependent geometric factor
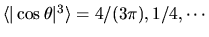 for
for 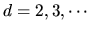 [46].
[46].
Figure:
The white-noise approximation estimate (WNA is the horizontal dotted line)
compared to actual
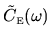 power spectra
for some example deformations of the 2D generalized Sinai
billiard, with
power spectra
for some example deformations of the 2D generalized Sinai
billiard, with 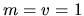 .
(The RMS estimation
error of 3% can be seen as
multiplicative noise with short correlation length in
.
(The RMS estimation
error of 3% can be seen as
multiplicative noise with short correlation length in 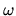 ).
The deformations (sketched on the right),
from worst to best agreement of the WNA are:
FR (for which sensitivity to the least-unstable vertical periodic orbit
causes large correlation effects and large deviations from WNA),
W8 (oscillatory deformation changes sign enough to be close to WNA),
P1 (localized `piston' type deformation for which WNA is good),
and
DF (random function of zero correlation-length along the
perimeter, showing complete WNA agreement).
Deformation functions are defined in Table 3.1.
).
The deformations (sketched on the right),
from worst to best agreement of the WNA are:
FR (for which sensitivity to the least-unstable vertical periodic orbit
causes large correlation effects and large deviations from WNA),
W8 (oscillatory deformation changes sign enough to be close to WNA),
P1 (localized `piston' type deformation for which WNA is good),
and
DF (random function of zero correlation-length along the
perimeter, showing complete WNA agreement).
Deformation functions are defined in Table 3.1.
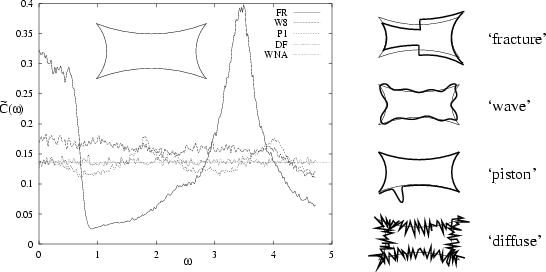 |
Table 3.1:
Key to deformation types used for numerical 2D billiard
experiments in this and the following chapter.
 is the billiard perimeter.
The deformation is described by a function
is the billiard perimeter.
The deformation is described by a function  ,
where
,
where  is measured counter-clockwise along the
perimeter with
is measured counter-clockwise along the
perimeter with 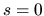 at the upper left corner. In the
`fracture' and `shift-x' cases we use the horizontal
Cartesian coordinate
at the upper left corner. In the
`fracture' and `shift-x' cases we use the horizontal
Cartesian coordinate 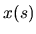 .
.
| key |
description |
surface deformation function 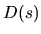 |
| CO |
constant |
1 |
W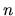 |
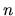 periods periods |
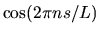 |
| DF |
diffuse |
random[-1,1] (equivalent to W ) ) |
| FR |
fracture |
sgn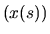 if on top or bottom, else 0 if on top or bottom, else 0 |
| SX |
shift-x |
sgn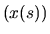 if on left or right, else 0 if on left or right, else 0 |
| P1 |
piston 1 |
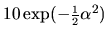 , ,
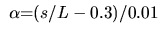 |
| P2 |
piston 2 |
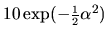 , ,
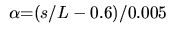 |
| WG |
wiggle |
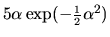 , ,
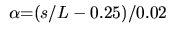 |
|



Next: The white noise approximation
Up: The cavity system
Previous: Form of correlation spectrum
Alex Barnett
2001-10-03
![]() in the next section,
but it can be skipped on first reading.
(It is presented in a more terse form in [46]).
in the next section,
but it can be skipped on first reading.
(It is presented in a more terse form in [46]).
