


Next: Form of correlation spectrum
Up: Chapter 3: Dissipation rate
Previous: Chapter 3: Dissipation rate
The cavity system
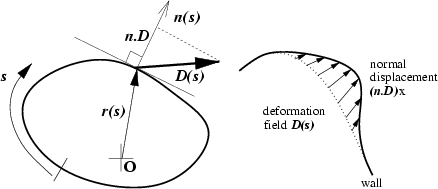
Figure:
Left:
Coordinates and local outward normal direction.
The boundary deformation function is
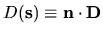 .
Right:
Action of deformation field on wall for finite parameter
.
Right:
Action of deformation field on wall for finite parameter 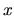 (the
undeformed wall for
(the
undeformed wall for 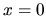 is shown by a dotted line).
is shown by a dotted line).
 |
Consider a single particle whose canonical coordinates
are
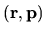 moving inside a cavity of
moving inside a cavity of 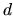 .
The Hamiltonian is
.
The Hamiltonian is
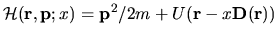 |
|
|
(3.1) |
where
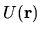 is the confining potential.
I have introduced a (unitless) deformation `field'
is the confining potential.
I have introduced a (unitless) deformation `field'
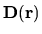 , so the effect of changing the
parameter
, so the effect of changing the
parameter 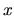 is to distort the potential in space.
We assume that
is to distort the potential in space.
We assume that
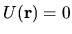 inside the cavity. Outside the cavity the
potential
inside the cavity. Outside the cavity the
potential
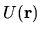 becomes very large.
To be specific, one may assume that the walls
exert a normal force
becomes very large.
To be specific, one may assume that the walls
exert a normal force 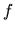 , and we take the
hard wall limit
, and we take the
hard wall limit
 .
With the above assumptions about
.
With the above assumptions about
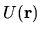 it is
clear that the deformation is completely specified
by the scalar boundary deformation function
it is
clear that the deformation is completely specified
by the scalar boundary deformation function
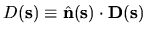 ,
where
,
where
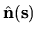 is an outwards
unit normal vector at the boundary point
is an outwards
unit normal vector at the boundary point 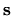 .
This is shown in Fig. 3.1.
The surface area of the cavity is
.
This is shown in Fig. 3.1.
The surface area of the cavity is 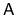 .
Its volume is
.
Its volume is 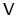 ,
which is related to its typical length
,
which is related to its typical length 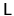 by
by
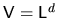 .
Quantum-mechanically, a second length scale
.
Quantum-mechanically, a second length scale
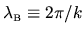 appears,
where
appears,
where 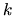 is the wavenumber.
The other parameters
is the wavenumber.
The other parameters
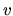 (particle velocity) and
(particle velocity) and 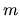 (particle mass),
as well as
(particle mass),
as well as 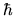 ,
could be scaled away
with the appropriate choice of units (this will only be done
in numerical tests where we set
,
could be scaled away
with the appropriate choice of units (this will only be done
in numerical tests where we set 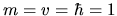 ).
The energy is
).
The energy is
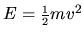 .
Sometimes I will use
.
Sometimes I will use
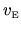 to denote
to denote 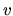 corresponding to energy
corresponding to energy 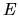 .
Upon quantization the eigenenergies, which in general are
.
Upon quantization the eigenenergies, which in general are
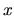 -dependent,
are
-dependent,
are
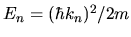 .
.
My numerical calculations of the band profile in this and the following chapter,
unless otherwise stated,
will refer to the two-dimensional (2D) cavity
illustrated in Fig. 3.2, which we call the generalized Sinai
billiard.
The shape has been chosen because
it has `hard chaos': no mixed phase space, and absence
of any marginally-stable orbits (see Section 3.4).
In Fig. 3.2b we show three example deformations of this billiard.
The band profile calculations will generally be done classically
(Appendix B), since
this is easier by far than the quantum calculation
(Appendix C). The two have been
demonstrated equivalent in Section 2.3.
In Section 3.3.2 I will verify this equivalence for
special deformations.
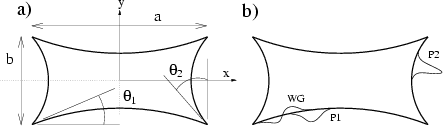
Figure 3.2:
a) The example (undeformed) cavity used for numerical studies
(unless otherwise stated): a
generalized two-dimensional Sinai billiard
formed from concave arcs of circles with two different radii.
Typical parameters used are 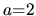 ,
, 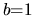 ,
,
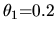 ,
,
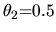 ,
for which the average collision rate with the wall is
,
for which the average collision rate with the wall is
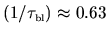 .
b) Sketches of the effect of three of the deformation types on the
perimeter (here we have chosen three localized deformations;
see Tables 3.1 and 3.2
for functional forms of all deformations used).
The deformations are shown exaggerated in strength.
.
b) Sketches of the effect of three of the deformation types on the
perimeter (here we have chosen three localized deformations;
see Tables 3.1 and 3.2
for functional forms of all deformations used).
The deformations are shown exaggerated in strength.
 |
Subsections



Next: Form of correlation spectrum
Up: Chapter 3: Dissipation rate
Previous: Chapter 3: Dissipation rate
Alex Barnett
2001-10-03


![]() moving inside a cavity of
moving inside a cavity of ![]() .
The Hamiltonian is
.
The Hamiltonian is
