


Next: Conversion of time averages
Up: The cavity system
Previous: The cavity system
Form of correlation spectrum and timescales
As presented in Section 2.1, the generalized time-dependent
`force' associated with the parameter 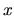 is
is
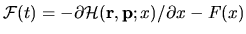 , where
, where 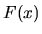 is
a constant such that the time-average is zero.
It has the
is
a constant such that the time-average is zero.
It has the
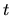 -independent auto-correlation function
-independent auto-correlation function
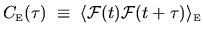 |
|
|
(3.2) |
The subscript
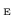 , whenever used, suggests that the
average over initial conditions is of microcanonical
type, with energy
, whenever used, suggests that the
average over initial conditions is of microcanonical
type, with energy 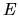 .
For the Hamiltonian (3.1) we can write
.
For the Hamiltonian (3.1) we can write
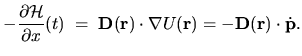 |
|
|
(3.3) |
Recognizing
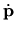 as the force on the gas particle,
we see that
as the force on the gas particle,
we see that
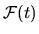 is a train of spikes superimposed on a constant
average value (see Fig. 3.3a):
is a train of spikes superimposed on a constant
average value (see Fig. 3.3a):
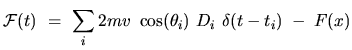 |
|
|
(3.4) |
where 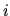 labels collisions:
labels collisions: 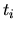 is the time of a collision,
is the time of a collision,
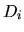 stands for
stands for
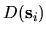 at the location
at the location 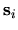 of a collision, and
of a collision, and
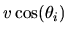 is the normal component of the particle's collision velocity.
If the deformation is volume-preserving then
is the normal component of the particle's collision velocity.
If the deformation is volume-preserving then
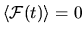 , otherwise it is
convenient to subtract the (constant) average value
, otherwise it is
convenient to subtract the (constant) average value 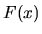 .
.
The auto-correlation function
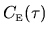 can be handled as a time-average of a single trajectory rather than
an ensemble-average over trajectories
(by ergodicity, as discussed in Section 2.1.6);
the resulting construction is
illustrated in Fig. 3.3b.
The forms of
can be handled as a time-average of a single trajectory rather than
an ensemble-average over trajectories
(by ergodicity, as discussed in Section 2.1.6);
the resulting construction is
illustrated in Fig. 3.3b.
The forms of
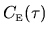 and
its Fourier transform
and
its Fourier transform
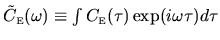 are illustrated schematically
in Figs. 3.3c and 3.3d.
The removal of the average value of
are illustrated schematically
in Figs. 3.3c and 3.3d.
The removal of the average value of
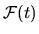 ensures that there is
no
ensures that there is
no  -function spike at
-function spike at 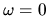 in
in
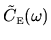 .
This is required so that
.
This is required so that
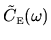 has a well-defined
has a well-defined
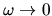 limit, namely the fluctuations intensity
limit, namely the fluctuations intensity
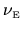 .
.
The auto-correlation function
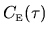 consists of a
consists of a 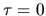 (`self')
peak due to the self-correlation of the
spikes, and of an additional smooth (`non-self') component due to
correlations between successive bounces.
(Note that in the hard walled limit the constant value
(`self')
peak due to the self-correlation of the
spikes, and of an additional smooth (`non-self') component due to
correlations between successive bounces.
(Note that in the hard walled limit the constant value 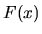 contributes nothing to the `self'
contributes nothing to the `self' 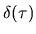 peak, so its only effect
is on the `non-self' component).
Thus two time scales
are involved: the short time scale is
peak, so its only effect
is on the `non-self' component).
Thus two time scales
are involved: the short time scale is
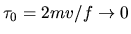 in the hard wall limit,
and the other time scale is
in the hard wall limit,
and the other time scale is
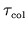 , which
involves the time for succesive collisions with the deforming
part of the boundary.
Note that
, which
involves the time for succesive collisions with the deforming
part of the boundary.
Note that
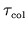 can
be much larger than the
ballistic time
can
be much larger than the
ballistic time
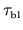 (the average time to cross
the billiard) in the case that only a small piece
of the boundary is being deformed.
The quantitative definition of the collision rate
(the average time to cross
the billiard) in the case that only a small piece
of the boundary is being deformed.
The quantitative definition of the collision rate
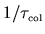 is postponed to Section 3.2.
is postponed to Section 3.2.
I shall be most interested in the noise intensity
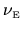 defined by (2.14).
Observing that
defined by (2.14).
Observing that
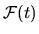 is linear in
is linear in
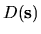 ,
it follows that the noise intensity must (exactly) be a general quadratic functional
,
it follows that the noise intensity must (exactly) be a general quadratic functional
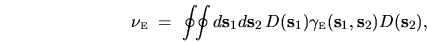 |
(3.5) |
where the kernel
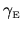 depends on both the
cavity shape and the particle energy
depends on both the
cavity shape and the particle energy 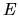 [120].
Furthermore, billiards
are scaling systems in the sense that a change in
[120].
Furthermore, billiards
are scaling systems in the sense that a change in 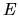 leaves the
trajectories unchanged.
From this and (3.4) we have the scaling relation
leaves the
trajectories unchanged.
From this and (3.4) we have the scaling relation
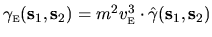 ,
where the scaled kernel depends entirely on the geometrical
shape of the cavity.
However, the reason for being interested in approximations for
,
where the scaled kernel depends entirely on the geometrical
shape of the cavity.
However, the reason for being interested in approximations for
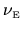 is that the exact result for the kernel
is that the exact result for the kernel 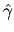 is not analytic: it is very complicated to evaluate, and
involves a sum over all classical paths from
is not analytic: it is very complicated to evaluate, and
involves a sum over all classical paths from 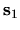 to
to 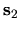 (see [120]).
(see [120]).
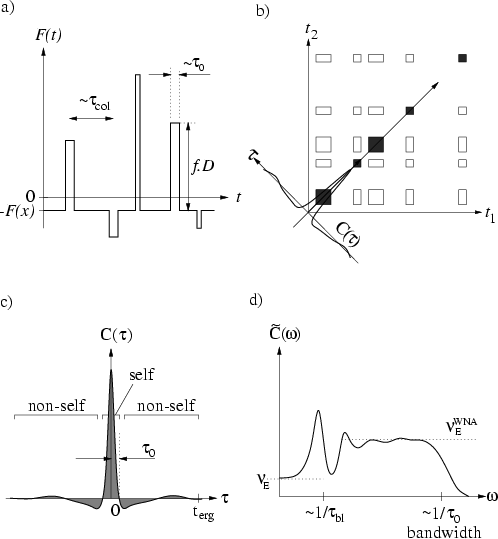
Figure:
a) The fluctuating force
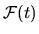 is a series of impulses
of maximum duration
is a series of impulses
of maximum duration 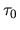 .
In the hard-walled limit
.
In the hard-walled limit
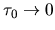 .
The average value
.
The average value 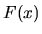 has been subtracted.
b) The autocorrelation function
has been subtracted.
b) The autocorrelation function 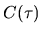 can be viewed
as the average projection of
the function
can be viewed
as the average projection of
the function
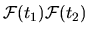 onto the
onto the
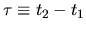 axis (the `self' components are shaded).
c) The autocorrelation function has a `self' peak of
half-width
axis (the `self' components are shaded).
c) The autocorrelation function has a `self' peak of
half-width 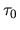 , and becomes negligible beyond
the ergodic time
, and becomes negligible beyond
the ergodic time
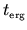 .
d) The noise power spectrum
.
d) The noise power spectrum
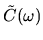 . Its
. Its
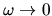 limit
is equal to the area under
limit
is equal to the area under 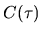 .
The power spectrum typically shows billiard-specific features
around the frequency
.
The power spectrum typically shows billiard-specific features
around the frequency
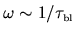 , where
, where
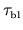 is the ballistic time.
Note that in some examples
is the ballistic time.
Note that in some examples
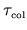 is much
longer than
is much
longer than
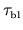 .
.
 |



Next: Conversion of time averages
Up: The cavity system
Previous: The cavity system
Alex Barnett
2001-10-03
![]() is
is
![]() , where
, where ![]() is
a constant such that the time-average is zero.
It has the
is
a constant such that the time-average is zero.
It has the
![]() -independent auto-correlation function
-independent auto-correlation function
![]() can be handled as a time-average of a single trajectory rather than
an ensemble-average over trajectories
(by ergodicity, as discussed in Section 2.1.6);
the resulting construction is
illustrated in Fig. 3.3b.
The forms of
can be handled as a time-average of a single trajectory rather than
an ensemble-average over trajectories
(by ergodicity, as discussed in Section 2.1.6);
the resulting construction is
illustrated in Fig. 3.3b.
The forms of
![]() and
its Fourier transform
and
its Fourier transform
![]() are illustrated schematically
in Figs. 3.3c and 3.3d.
The removal of the average value of
are illustrated schematically
in Figs. 3.3c and 3.3d.
The removal of the average value of
![]() ensures that there is
no
ensures that there is
no ![]() -function spike at
-function spike at ![]() in
in
![]() .
This is required so that
.
This is required so that
![]() has a well-defined
has a well-defined
![]() limit, namely the fluctuations intensity
limit, namely the fluctuations intensity
![]() .
.
![]() consists of a
consists of a ![]() (`self')
peak due to the self-correlation of the
spikes, and of an additional smooth (`non-self') component due to
correlations between successive bounces.
(Note that in the hard walled limit the constant value
(`self')
peak due to the self-correlation of the
spikes, and of an additional smooth (`non-self') component due to
correlations between successive bounces.
(Note that in the hard walled limit the constant value ![]() contributes nothing to the `self'
contributes nothing to the `self' ![]() peak, so its only effect
is on the `non-self' component).
Thus two time scales
are involved: the short time scale is
peak, so its only effect
is on the `non-self' component).
Thus two time scales
are involved: the short time scale is
![]() in the hard wall limit,
and the other time scale is
in the hard wall limit,
and the other time scale is
![]() , which
involves the time for succesive collisions with the deforming
part of the boundary.
Note that
, which
involves the time for succesive collisions with the deforming
part of the boundary.
Note that
![]() can
be much larger than the
ballistic time
can
be much larger than the
ballistic time
![]() (the average time to cross
the billiard) in the case that only a small piece
of the boundary is being deformed.
The quantitative definition of the collision rate
(the average time to cross
the billiard) in the case that only a small piece
of the boundary is being deformed.
The quantitative definition of the collision rate
![]() is postponed to Section 3.2.
is postponed to Section 3.2.
![]() defined by (2.14).
Observing that
defined by (2.14).
Observing that
![]() is linear in
is linear in
![]() ,
it follows that the noise intensity must (exactly) be a general quadratic functional
,
it follows that the noise intensity must (exactly) be a general quadratic functional
