


Next: Energy spreading periodic driving
Up: Review of classical dissipation
Previous: Adiabatic invariance of phase-space
Energy spreading--constant velocity case
We now derive the next-order correction to the adiabatic limit,
namely spreading in energy (or equivalently in 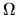 ),
which causes the
irreversible heating.
This was first found by Ott [153] using `multiple-time-scale analysis'.
To derive the spreading rate,
we now assume
constant parameter velocity
),
which causes the
irreversible heating.
This was first found by Ott [153] using `multiple-time-scale analysis'.
To derive the spreading rate,
we now assume
constant parameter velocity 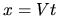 over a time interval
long enough to establish diffusive behaviour
(following [47,46]).
The longer-time evolution for a general
over a time interval
long enough to establish diffusive behaviour
(following [47,46]).
The longer-time evolution for a general 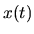 can
then be built from these short constant-velocity segments.
can
then be built from these short constant-velocity segments.
For any given particle trajectory
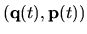 (ensemble member
launched at
(ensemble member
launched at
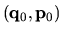 at
at 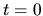 )
there is an associated stochastic time-dependent `force'
)
there is an associated stochastic time-dependent `force'
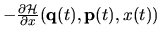 on the parameter
on the parameter 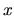 .
The time-dependence arises from that of the trajectory.
In the billiard case, this is simply the impulses
the particle exerts on the deforming part of the wall.
We extract the fluctuation of this quantity about
its average (which from (2.3) is just the conservative
force
.
The time-dependence arises from that of the trajectory.
In the billiard case, this is simply the impulses
the particle exerts on the deforming part of the wall.
We extract the fluctuation of this quantity about
its average (which from (2.3) is just the conservative
force 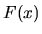 ), giving the definition
), giving the definition
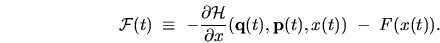 |
(2.6) |
The external work done in changing the parameter from 0 to 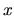 can
be found by integrating force over distance to give
can
be found by integrating force over distance to give
![$Q = - \int_0^x dx' [ {\mathcal{F}}(t(x')) + F(x') ]$](img135.gif) ,
which must be converted to an increase in the
particle energy.
Writing this as a time integral, the
particle's energy difference at time
,
which must be converted to an increase in the
particle energy.
Writing this as a time integral, the
particle's energy difference at time 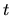 from the adiabatic value
from the adiabatic value 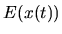 is
is
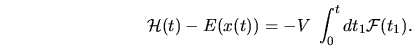 |
(2.7) |
Now
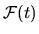 has a finite correlation time
has a finite correlation time
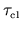 which is
similar to or less than the ergodic time.
For
which is
similar to or less than the ergodic time.
For
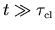 then the above expression is
simply the final energy change resulting from a `random walk' of step size
then the above expression is
simply the final energy change resulting from a `random walk' of step size
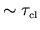 .
Squaring this and taking a microcanonical average
(at energy
.
Squaring this and taking a microcanonical average
(at energy 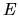 )
gives the energy variance
)
gives the energy variance
This last approximation is good for
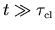 ,
where the double integral grows linearly
in
,
where the double integral grows linearly
in 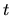 (with fractional error from linearity dying like
(with fractional error from linearity dying like
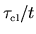 ).
This is simply the variance of a random walk growing linearly in time.
It can also be shown using a transform of variables to
).
This is simply the variance of a random walk growing linearly in time.
It can also be shown using a transform of variables to
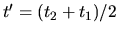 and
and
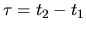 ,
with the range of
,
with the range of 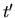 being
being ![$[0,t]$](img151.gif) , and
the range of
, and
the range of 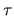 can be taken to
can be taken to
![$[-\infty,\infty]$](img153.gif) ,
as illustrated in Fig. 2.2a.
We will write
,
as illustrated in Fig. 2.2a.
We will write
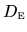 in terms of
in terms of
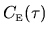 , the
autocorrelation function of the fluctuating force.
, the
autocorrelation function of the fluctuating force.
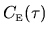 depends on both the classical motion at
energy
depends on both the classical motion at
energy 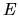 and on the particular deformation chosen,
and is defined by
and on the particular deformation chosen,
and is defined by
where the second equality states the assumption
that the autocorrelation does not change over the
timescale 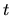 .
This latter condition restricts
.
This latter condition restricts 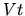 to be much smaller than
to be much smaller than
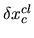 , the parametric change which
changes the classical Hamiltonian (and hence the statistical
properties of the system) significantly.
In combination with the limit
, the parametric change which
changes the classical Hamiltonian (and hence the statistical
properties of the system) significantly.
In combination with the limit
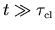 ,
this gives
,
this gives
 |
(2.12) |
(this is the `trivial slowness condition' of Cohen [46]).
We now have established diffusive energy spreading
with a rate
(given by substitution of (2.10) into (2.8))
of
 |
(2.13) |
where
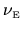 is the (zero-frequency) ``noise intensity''
of the fluctuating force,
equal to the first moment of the autocorrelation function:
is the (zero-frequency) ``noise intensity''
of the fluctuating force,
equal to the first moment of the autocorrelation function:
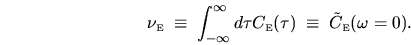 |
(2.14) |
The correlation power spectrum or
spectral density of
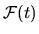 is called
is called
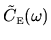 , and is the fourier transform of the
autocorrelation function. I use the convention
, and is the fourier transform of the
autocorrelation function. I use the convention
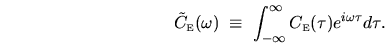 |
(2.15) |
Now that diffusion is
established for short time-steps  ,
the evolution over longer times with a general
,
the evolution over longer times with a general 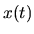 can be composed of independent diffusive steps
each operating on the probability distribution
can be composed of independent diffusive steps
each operating on the probability distribution 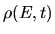 given by the previous step.
This `memory-less' stochastic approximation is called Markovian
[79].
Note that, in this picture,
if
given by the previous step.
This `memory-less' stochastic approximation is called Markovian
[79].
Note that, in this picture,
if 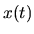 ever becomes comparable to
ever becomes comparable to
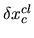 then the diffusion rate should be treated as parameter-dependent
then the diffusion rate should be treated as parameter-dependent
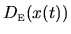 .
.
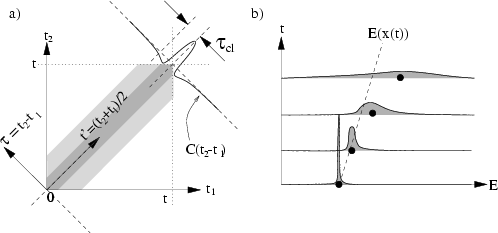
Figure:
a) Plot of the microcanonical average of
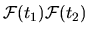 , showing how its
double integral (Eq. 2.8)
from time 0 to
, showing how its
double integral (Eq. 2.8)
from time 0 to 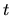 can be rewritten as
can be rewritten as 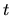 times the
first moment of the autocorrelation function
times the
first moment of the autocorrelation function
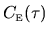 .
.
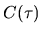 itself is shown shaded, and it is significant only for
itself is shown shaded, and it is significant only for
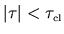 .
b) Evolution of
.
b) Evolution of 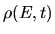 (shaded) showing drift and diffusion.
Energy-dependence of both the diffusion constant and
the density of states causes an asymmetric distribution, and additional
drift.
This causes the centroid
(shaded) showing drift and diffusion.
Energy-dependence of both the diffusion constant and
the density of states causes an asymmetric distribution, and additional
drift.
This causes the centroid
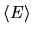 (shown by black dot) to be become higher than the adiabatic value
(shown by black dot) to be become higher than the adiabatic value 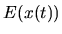 (shown by dashed line).
This drift never becomes larger than the width due to spreading.
(shown by dashed line).
This drift never becomes larger than the width due to spreading.
 |



Next: Energy spreading periodic driving
Up: Review of classical dissipation
Previous: Adiabatic invariance of phase-space
Alex Barnett
2001-10-03
![]() ),
which causes the
irreversible heating.
This was first found by Ott [153] using `multiple-time-scale analysis'.
To derive the spreading rate,
we now assume
constant parameter velocity
),
which causes the
irreversible heating.
This was first found by Ott [153] using `multiple-time-scale analysis'.
To derive the spreading rate,
we now assume
constant parameter velocity ![]() over a time interval
long enough to establish diffusive behaviour
(following [47,46]).
The longer-time evolution for a general
over a time interval
long enough to establish diffusive behaviour
(following [47,46]).
The longer-time evolution for a general ![]() can
then be built from these short constant-velocity segments.
can
then be built from these short constant-velocity segments.
![]() (ensemble member
launched at
(ensemble member
launched at
![]() at
at ![]() )
there is an associated stochastic time-dependent `force'
)
there is an associated stochastic time-dependent `force'
![]() on the parameter
on the parameter ![]() .
The time-dependence arises from that of the trajectory.
In the billiard case, this is simply the impulses
the particle exerts on the deforming part of the wall.
We extract the fluctuation of this quantity about
its average (which from (2.3) is just the conservative
force
.
The time-dependence arises from that of the trajectory.
In the billiard case, this is simply the impulses
the particle exerts on the deforming part of the wall.
We extract the fluctuation of this quantity about
its average (which from (2.3) is just the conservative
force ![]() ), giving the definition
), giving the definition
