


Next: Fokker-Planck equation for energy
Up: Review of classical dissipation
Previous: Energy spreading constant velocity
Energy spreading--periodic driving case
We can build on the results of the previous section to
see how things change if the parameteric driving
is sinusoidal:
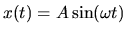 .
We will find the new spreading rate
.
We will find the new spreading rate
 in the same fashion.
For a general
in the same fashion.
For a general  , Eq. (2.7) becomes
, Eq. (2.7) becomes
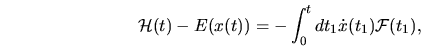 |
(2.16) |
As before, squaring this and taking the microcanonical average gives
On the second line above,
the same transformation of time variables was used as before
(Fig. 2.2a, except now multiplied by the `checkerboard'
of the cos functions),
and the 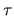 range expanded as before to
range expanded as before to
![$[-\infty,\infty]$](img153.gif) ,
appropriate when
,
appropriate when
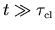 .
The final line shows an oscillating term
and a diffusive term (linear in
.
The final line shows an oscillating term
and a diffusive term (linear in 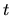 ),
and is valid for any
),
and is valid for any 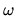 .
The diffusion
becomes dominant in the limit
.
The diffusion
becomes dominant in the limit
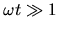 corresponding
to observation over a large number of parameter oscillation periods
(the fractional error due to the oscillating term dying like
corresponding
to observation over a large number of parameter oscillation periods
(the fractional error due to the oscillating term dying like
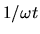 ),
giving linear growth of the second moment.
This long-time diffusion rate is
),
giving linear growth of the second moment.
This long-time diffusion rate is
 |
(2.18) |
where 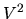 is now defined as the mean square parameter velocity
is now defined as the mean square parameter velocity
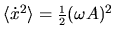 .
.
So it is apparent that the diffusion is determined by the
spectral density of
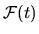 at the driving frequency.
As this frequency goes to zero, the linear driving result (2.13)
is recovered.
This can be verified by taking the limit
at the driving frequency.
As this frequency goes to zero, the linear driving result (2.13)
is recovered.
This can be verified by taking the limit
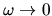 while
while
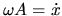 is held constant, using
is held constant, using
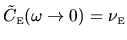 ,
and noticing that
the two terms in (2.17) now contribute equally.
,
and noticing that
the two terms in (2.17) now contribute equally.



Next: Fokker-Planck equation for energy
Up: Review of classical dissipation
Previous: Energy spreading constant velocity
Alex Barnett
2001-10-03
![]() .
We will find the new spreading rate
.
We will find the new spreading rate
![]() in the same fashion.
For a general
in the same fashion.
For a general ![]() , Eq. (2.7) becomes
, Eq. (2.7) becomes
![]() at the driving frequency.
As this frequency goes to zero, the linear driving result (2.13)
is recovered.
This can be verified by taking the limit
at the driving frequency.
As this frequency goes to zero, the linear driving result (2.13)
is recovered.
This can be verified by taking the limit
![]() while
while
![]() is held constant, using
is held constant, using
![]() ,
and noticing that
the two terms in (2.17) now contribute equally.
,
and noticing that
the two terms in (2.17) now contribute equally.