


Next: Irreversible growth of average
Up: Review of classical dissipation
Previous: Energy spreading periodic driving
Fokker-Planck equation for energy evolution
Stochastic evolution is generally governed by a Fokker-Planck equation,
describing
drift and diffusion of a density function (see Appendix A
and [79]).
The derivation of the correct Fokker-Planck equation
for the time-evolution of the
energy distribution 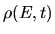 is not trivial.
Now that we have the energy diffusion rate
is not trivial.
Now that we have the energy diffusion rate
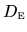 at a given energy
at a given energy 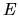 , it is
tempting to use it directly as a standard (energy-dependent)
diffusion term
, it is
tempting to use it directly as a standard (energy-dependent)
diffusion term
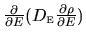 .
This simple answer is wrong, and would give the wrong heating rate.
As discussed in Appendix A, care is needed in
writing the diffusion term.
The equation was first written down correctly (without derivation)
by Wilkinson [201].
Jarzynski [106] derives
it in a clear fashion (which I will follow), and later he [108]
and Berry and Robbins
[27] rederive it using expansions
of the full phase-space density in powers of a `slowness parameter'
(
.
This simple answer is wrong, and would give the wrong heating rate.
As discussed in Appendix A, care is needed in
writing the diffusion term.
The equation was first written down correctly (without derivation)
by Wilkinson [201].
Jarzynski [106] derives
it in a clear fashion (which I will follow), and later he [108]
and Berry and Robbins
[27] rederive it using expansions
of the full phase-space density in powers of a `slowness parameter'
(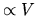 ).
).
It must be realised that, although the spreading rate was derived in energy,
it is 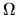 that is the `natural' variable in which to discuss spreading.
Not only is the evolution of
that is the `natural' variable in which to discuss spreading.
Not only is the evolution of
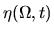 simple,
but the consideration of Liouville's theorem becomes obvious.
In the adiabatic limit
simple,
but the consideration of Liouville's theorem becomes obvious.
In the adiabatic limit 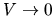 we have seen that
we have seen that
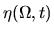 is constant (2.5).
At finite
is constant (2.5).
At finite 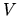 the evolution generally becomes
the evolution generally becomes
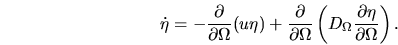 |
(2.19) |
Liouville's equation of motion [126] for
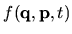 ,
the full phase-space probability density, is
,
the full phase-space probability density, is
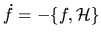 .
Regardless of the Hamiltonian and its time-dependence,
this means that a constant
density must remain so for all times.
Recalling that
.
Regardless of the Hamiltonian and its time-dependence,
this means that a constant
density must remain so for all times.
Recalling that 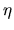 is just the average of
is just the average of 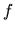 over an energy-shell,
this means
over an energy-shell,
this means
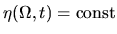 must
be a solution of (2.19).
It must also be a solution
with zero flux
must
be a solution of (2.19).
It must also be a solution
with zero flux 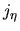 everywhere in
everywhere in 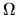 (if this we not so, a discontinuity
would arise at
(if this we not so, a discontinuity
would arise at 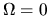 ; see also Appendix B of [106] ).
This implies that in (2.19) the drift term
; see also Appendix B of [106] ).
This implies that in (2.19) the drift term 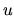 is zero,
and the diffusion is unbiased in
is zero,
and the diffusion is unbiased in 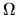 -space.
By `unbiased' I mean that at every value of
-space.
By `unbiased' I mean that at every value of 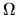 ,
zero density gradient results in zero flux.
Note that the
,
zero density gradient results in zero flux.
Note that the 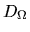 may still depend on
may still depend on 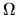 .
.
Now this ``Liouville trick'' has been performed, we can transform
the evolution back to energy-space;
this is done using Appendix A, and gives
a Fokker-Planck equation with non-zero drift,
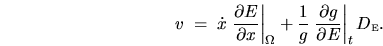 |
(2.20) |
The first term gives the usual adiabatic energy change, while the second
is a drift term entirely due to diffusion.
This gives the final energy evolution, written with the
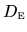 terms
grouped together to give a modified diffusion term,
terms
grouped together to give a modified diffusion term,
![\begin{displaymath}
\dot{\rho} \; = \; -\dot{x} \frac{\partial }{\partial E}
\...
...{\partial }{\partial E} \left( \frac{\rho}{g} \right) \right].
\end{displaymath}](img200.gif) |
(2.21) |
Remember that (2.21)
is an effective equation for timescales longer than
the ergodic time.
In the context of billiards, energy evolution
can be thought of as the
biased `random walk' in energy space due to the
sum of `kicks' due to the particle hitting the moving walls [107].



Next: Irreversible growth of average
Up: Review of classical dissipation
Previous: Energy spreading periodic driving
Alex Barnett
2001-10-03
![]() is not trivial.
Now that we have the energy diffusion rate
is not trivial.
Now that we have the energy diffusion rate
![]() at a given energy
at a given energy ![]() , it is
tempting to use it directly as a standard (energy-dependent)
diffusion term
, it is
tempting to use it directly as a standard (energy-dependent)
diffusion term
![]() .
This simple answer is wrong, and would give the wrong heating rate.
As discussed in Appendix A, care is needed in
writing the diffusion term.
The equation was first written down correctly (without derivation)
by Wilkinson [201].
Jarzynski [106] derives
it in a clear fashion (which I will follow), and later he [108]
and Berry and Robbins
[27] rederive it using expansions
of the full phase-space density in powers of a `slowness parameter'
(
.
This simple answer is wrong, and would give the wrong heating rate.
As discussed in Appendix A, care is needed in
writing the diffusion term.
The equation was first written down correctly (without derivation)
by Wilkinson [201].
Jarzynski [106] derives
it in a clear fashion (which I will follow), and later he [108]
and Berry and Robbins
[27] rederive it using expansions
of the full phase-space density in powers of a `slowness parameter'
(![]() ).
).
![]() that is the `natural' variable in which to discuss spreading.
Not only is the evolution of
that is the `natural' variable in which to discuss spreading.
Not only is the evolution of
![]() simple,
but the consideration of Liouville's theorem becomes obvious.
In the adiabatic limit
simple,
but the consideration of Liouville's theorem becomes obvious.
In the adiabatic limit ![]() we have seen that
we have seen that
![]() is constant (2.5).
At finite
is constant (2.5).
At finite ![]() the evolution generally becomes
the evolution generally becomes