


Next: Appendix B: Numerical evaluation
Up: Dissipation in Deforming Chaotic
Previous: Conclusion
Appendix A: General transformation of the 1D Fokker-Planck equation
In this Appendix, I show how the drift and diffusion terms
in a general Fokker-Planck equation [79] for evolution
of a probability density function (PDF)
transform
when the variable (i.e. the spatial ordinate of the PDF) is transformed.
It is an essential step to understanding
the relation between ergodic energy spreading
in the energy variable 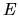 (in which the diffusion constant is
most easily found) and in
the enclosed-phase-space-volume variable
(in which the diffusion constant is
most easily found) and in
the enclosed-phase-space-volume variable 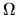 (the natural variable for discussing spreading
because of its conservation under Liouville's theorem).
I present known results; in particular, the results derived here
are assumed by Jarzynski [106] and Cohen [46].
However it is complicated enough, especially in the case of
a time-dependent density of states, to merit a clear explanation.
(the natural variable for discussing spreading
because of its conservation under Liouville's theorem).
I present known results; in particular, the results derived here
are assumed by Jarzynski [106] and Cohen [46].
However it is complicated enough, especially in the case of
a time-dependent density of states, to merit a clear explanation.
We start with a known evolution
of the PDF
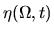 in
in 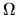 -space, and
want to find the equivalent evolution of
-space, and
want to find the equivalent evolution of 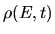 ,
the PDF in
,
the PDF in 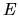 -space which describes the same situation.
We assume a one-to-one time-dependent mapping
-space which describes the same situation.
We assume a one-to-one time-dependent mapping
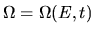 ,
which can be represented as a (fixed) surface in
three-dimensional
,
which can be represented as a (fixed) surface in
three-dimensional 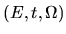 space (Fig. A.1).
Therefore
space (Fig. A.1).
Therefore
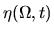 and
and 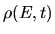 are projections
of the same function on the 3D surface, down the
are projections
of the same function on the 3D surface, down the 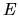 and
and 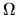 directions respectively.
The PDFs are related as follows,
directions respectively.
The PDFs are related as follows,
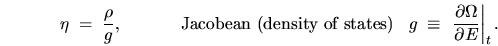 |
(A.1) |
From now on I will use prime to denote spatial derivative and dot time
derivative, in the natural variables of each PDF. Namely,
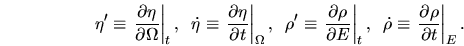 |
(A.2) |
Time-dependence will not be written explicitly. Partial derivatives will be
taken with  held constant unless otherwise specified.
held constant unless otherwise specified.
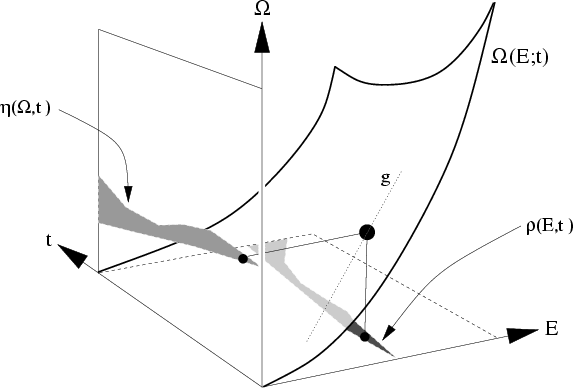
Figure A.1:
Projecting a probability density on the surface 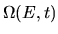 down to
down to 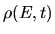 in the
in the 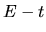 plane,
or across to
plane,
or across to
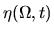 in the
in the 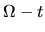 plane.
The gradient
plane.
The gradient 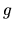 is also shown.
is also shown.
 |
The Fokker-Planck equations in the two variables arise as follows.
The probability fluxes (i.e. probability per unit time
flowing past a fixed point) are assumed linear in the local density and
its local gradient:
For the PDF 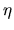 , the coefficient
, the coefficient 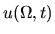 is a
`drift velocity' field and
is a
`drift velocity' field and 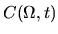 is a diffusion rate (both are generally space- and time-dependent).
For the PDF
is a diffusion rate (both are generally space- and time-dependent).
For the PDF 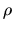 , similarly,
, similarly,
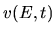 is the drift velocity and
is the drift velocity and 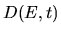 the diffusion rate.
We also have the probability conservation laws,
the diffusion rate.
We also have the probability conservation laws,
Combining (A.3) and (A.5) gives the Fokker-Planck
equation obeyed by 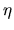 ,
,
 |
(A.7) |
Similarly the Fokker-Planck
equation obeyed by 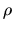 is,
is,
 |
(A.8) |
Given functions 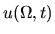 ,
, 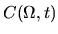 and (A.7),
our task is to find
and (A.7),
our task is to find
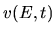 and
and 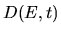 such that (A.8) and the
Jacobean transformation (A.1) are obeyed for all time.
The Jacobean results in the following rule for transforming derivatives:
such that (A.8) and the
Jacobean transformation (A.1) are obeyed for all time.
The Jacobean results in the following rule for transforming derivatives:
 |
(A.9) |
Use of this and of (A.1) allows (A.7) to be written as
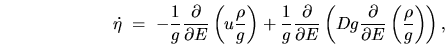 |
(A.10) |
where we have identified the transformed diffusion rate 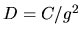 .
Note that the diffusion term has a modified form, which we examine later.
The LHS now poses a problem.
It is possible to transform the LHS, written as
.
Note that the diffusion term has a modified form, which we examine later.
The LHS now poses a problem.
It is possible to transform the LHS, written as
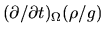 ,
using the Legendre rule for a change of
variable:
,
using the Legendre rule for a change of
variable:
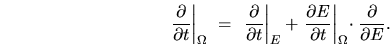 |
(A.11) |
However the resulting sequence of algebra
required to reach the desired form is very complicatedA.1and I will not give it here.
Instead I give a geometric approach which bypasses the algebra.
We ask how the probability fluxes are related.
If 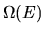 were independent of time,
were independent of time,
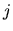 would transform without a Jacobean,
that is
would transform without a Jacobean,
that is
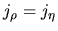 .
Now with
.
Now with 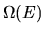 time-dependent,
time-dependent,
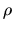 acquires an extra drift velocity
equal to the gradient of the constant-
acquires an extra drift velocity
equal to the gradient of the constant-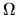 contour in the
contour in the 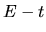 plane:
plane:
 |
(A.12) |
This can easily be verified by considering Fig. A.1.
The apparent lack of 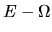 symmetry in this relation is deceptive
since the second (flux difference) term
can also be written
symmetry in this relation is deceptive
since the second (flux difference) term
can also be written
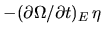 using
the relation
using
the relation
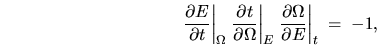 |
(A.13) |
which is a geometric property of any surface in 3D.
Combining (A.12) with (A.5), (A.6)
and (A.9) immediately gives
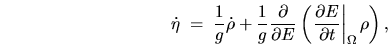 |
(A.14) |
which can now be substituted into the LHS of (A.10) to give
the desired Fokker-Planck evolution (A.8).
The resulting transformed coefficients are
Looking at the transformed drift,
the first term is the (scaled) original drift rate,
the second is `dragging' due to time-dependence of 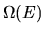 ,
and the third, which can also be written as
,
and the third, which can also be written as 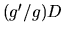 ,
is a drift term entirely due to the modification of the diffusion term.
The second term, being (minus) the parameter velocity
,
is a drift term entirely due to the modification of the diffusion term.
The second term, being (minus) the parameter velocity 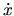 times the conservative
force
times the conservative
force
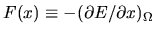 ,
will only cause reversible energy changes.
Note that the third term arises from the the transformation of the diffusion
term
,
will only cause reversible energy changes.
Note that the third term arises from the the transformation of the diffusion
term
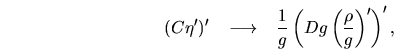 |
(A.17) |
In general, we see that a transformed diffusion term takes
the form of the right-hand side
of (A.17),
which is biased.
By `biased' I mean that it has nonzero local drift when there is zero
local density gradient.
The bias can be visualized if we imagine that diffusion in 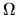 -space comes from
a the continuum limit of an unbiased
random walk on a uniformly-spaced lattice of sites.
The same sites appear non-uniformly spaced in
-space comes from
a the continuum limit of an unbiased
random walk on a uniformly-spaced lattice of sites.
The same sites appear non-uniformly spaced in 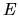 -space, so the same random walk
gives additional drift for the PDF in
-space, so the same random walk
gives additional drift for the PDF in 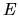 -space.
Only when a diffusion term is written in terms
of its `natural' variable (here
-space.
Only when a diffusion term is written in terms
of its `natural' variable (here 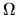 ) does it take the
unbiased form of the left-hand side of
(A.17).
This illustrates that great care should be taken in writing down an energy
diffusion term in the theory of energy spreading.
) does it take the
unbiased form of the left-hand side of
(A.17).
This illustrates that great care should be taken in writing down an energy
diffusion term in the theory of energy spreading.



Next: Appendix B: Numerical evaluation
Up: Dissipation in Deforming Chaotic
Previous: Conclusion
Alex Barnett
2001-10-03
![]() (in which the diffusion constant is
most easily found) and in
the enclosed-phase-space-volume variable
(in which the diffusion constant is
most easily found) and in
the enclosed-phase-space-volume variable ![]() (the natural variable for discussing spreading
because of its conservation under Liouville's theorem).
I present known results; in particular, the results derived here
are assumed by Jarzynski [106] and Cohen [46].
However it is complicated enough, especially in the case of
a time-dependent density of states, to merit a clear explanation.
(the natural variable for discussing spreading
because of its conservation under Liouville's theorem).
I present known results; in particular, the results derived here
are assumed by Jarzynski [106] and Cohen [46].
However it is complicated enough, especially in the case of
a time-dependent density of states, to merit a clear explanation.
![]() in
in ![]() -space, and
want to find the equivalent evolution of
-space, and
want to find the equivalent evolution of ![]() ,
the PDF in
,
the PDF in ![]() -space which describes the same situation.
We assume a one-to-one time-dependent mapping
-space which describes the same situation.
We assume a one-to-one time-dependent mapping
![]() ,
which can be represented as a (fixed) surface in
three-dimensional
,
which can be represented as a (fixed) surface in
three-dimensional ![]() space (Fig. A.1).
Therefore
space (Fig. A.1).
Therefore
![]() and
and ![]() are projections
of the same function on the 3D surface, down the
are projections
of the same function on the 3D surface, down the ![]() and
and ![]() directions respectively.
The PDFs are related as follows,
directions respectively.
The PDFs are related as follows,

![]() ,
, ![]() and (A.7),
our task is to find
and (A.7),
our task is to find
![]() and
and ![]() such that (A.8) and the
Jacobean transformation (A.1) are obeyed for all time.
The Jacobean results in the following rule for transforming derivatives:
such that (A.8) and the
Jacobean transformation (A.1) are obeyed for all time.
The Jacobean results in the following rule for transforming derivatives:
![]() were independent of time,
were independent of time,
![]() would transform without a Jacobean,
that is
would transform without a Jacobean,
that is
![]() .
Now with
.
Now with ![]() time-dependent,
time-dependent,
![]() acquires an extra drift velocity
equal to the gradient of the constant-
acquires an extra drift velocity
equal to the gradient of the constant-![]() contour in the
contour in the ![]() plane:
plane: