Now I explain the observed
![]() for special deformations,
using classical considerations.
The interested reader should also consult Appendix D.
I start with the case of translations and dilations.
For translations we have
for special deformations,
using classical considerations.
The interested reader should also consult Appendix D.
I start with the case of translations and dilations.
For translations we have
![]() ,
where
,
where ![]() is a constant vector
that defines a direction in space. We can write
is a constant vector
that defines a direction in space. We can write
![]() where
where
![]() .
A similar relation holds for dilation
.
A similar relation holds for dilation
![]() with
with
![]() . It follows that
. It follows that
![]() ,
where
,
where
![]() is the power spectrum
of
is the power spectrum
of
![]() .
If
.
If
![]() is a bounded function (as it must
be when correlations are short-range),
it immediately follows that
is a bounded function (as it must
be when correlations are short-range),
it immediately follows that
![]() .
Moreover since
.
Moreover since
![]() is a simple
function of the particle position, we can assume it is a
fluctuating quantity that looks like white
noise on timescales
is a simple
function of the particle position, we can assume it is a
fluctuating quantity that looks like white
noise on timescales
![]() .
It follows that
.
It follows that
![]() is
generically characterized by
is
generically characterized by ![]() behavior
for either translations or dilations.
behavior
for either translations or dilations.
I now consider the case of rotations.
For rotations we have
![]() ,
and we can write
,
and we can write
![]() ,
where
,
where
![]() ,
is a projection of the particle's angular momentum vector
3.2.
Consequently
,
is a projection of the particle's angular momentum vector
3.2.
Consequently
![]() .
Assuming the angular momentum is a
fluctuating quantity that looks like white
noise on timescales
.
Assuming the angular momentum is a
fluctuating quantity that looks like white
noise on timescales
![]() ,
we expect that
,
we expect that
![]() and that
and that
![]() is
generically characterized by
is
generically characterized by ![]() behavior.
behavior.
Thus we have predictions for the power-laws in
the regime
![]() for special deformations
(assuming hard chaos).
This contrasts the generic case of
tending to a constant, that is,
for special deformations
(assuming hard chaos).
This contrasts the generic case of
tending to a constant, that is, ![]() behavior.
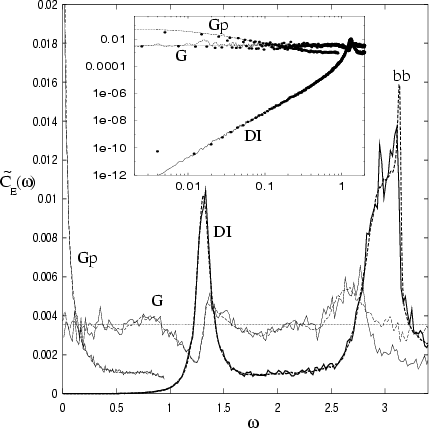
These power laws are demonstrated in Fig. 3.6,
and have been numerically verified over more than 4 decades in
behavior.
These power laws are demonstrated in Fig. 3.6,
and have been numerically verified over more than 4 decades in ![]() .
For an estimate of the prefactor for the dilation case, see
Section 6.1.2.
.
For an estimate of the prefactor for the dilation case, see
Section 6.1.2.
For special deformations we have
![]() in the limit
in the limit ![]() ,
and consequently the dissipation
coefficient vanishes (
,
and consequently the dissipation
coefficient vanishes (![]() ).
It should be noted that for the case of
a general combination of translations and rotations
this result
follows from a simpler argument
(one which does not rely on the LRT assumption considered in
[120,118]).
Taking
).
It should be noted that for the case of
a general combination of translations and rotations
this result
follows from a simpler argument
(one which does not rely on the LRT assumption considered in
[120,118]).
Taking
![]() while keeping
while keeping ![]() constant corresponds to
constant deformation velocity (
constant corresponds to
constant deformation velocity (![]() const).
Transforming the time-dependent Hamiltonian into the reference
frame of the cavity (which is uniformly translating
and rotating with constant velocity)
gives a time-independent Hamiltonian.
In the new reference frame the energy is a constant
of the motion, which implies that the system
cannot absorb energy (no dissipation effect),
and hence we must indeed have
const).
Transforming the time-dependent Hamiltonian into the reference
frame of the cavity (which is uniformly translating
and rotating with constant velocity)
gives a time-independent Hamiltonian.
In the new reference frame the energy is a constant
of the motion, which implies that the system
cannot absorb energy (no dissipation effect),
and hence we must indeed have ![]() .
.
 |