


Next: Scaling potentials and the
Up: Appendix D: How Many
Previous: Requirement on time-integral of
We start with the general potential case (with constant
isotropic mass).
The deformation field
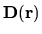 must be defined everywhere in space
(note that it does not change in time).
The deformation parameter
must be defined everywhere in space
(note that it does not change in time).
The deformation parameter 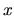 controls the hamiltonian
controls the hamiltonian
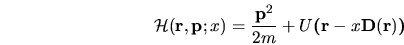 |
(D.4) |
by distorting the potential in space.
Note that there is already an infinite class of `trivially special'
deformation fields
such that
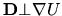 everywhere: these cause no
deformation.
Therefore a scalar field
everywhere: these cause no
deformation.
Therefore a scalar field
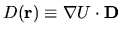 is sufficient to uniquely define the deformation.
However working
with the vector field
is sufficient to uniquely define the deformation.
However working
with the vector field
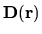 is more convenient
because every function
is more convenient
because every function
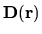 is a valid deformation.
(Not every
function
is a valid deformation.
(Not every
function
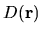 is valid; consider regions of constant potential).
At a frozen (fixed)
is valid; consider regions of constant potential).
At a frozen (fixed) 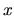 value, the fluctuating
force on the
value, the fluctuating
force on the 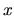 parameter, defined by (2.6), can be written
parameter, defined by (2.6), can be written
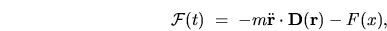 |
(D.5) |
where
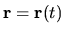 is the (time-dependent) particle position,
and
is the (time-dependent) particle position,
and
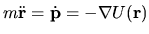 is the force on the particle.
Therefore
is the force on the particle.
Therefore 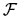 is a function of the particle position alone.
The constant
is a function of the particle position alone.
The constant 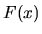 is chosen such
that the time-average of
is chosen such
that the time-average of 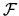 is zero;
this is necessary for the asymptotic value
is zero;
this is necessary for the asymptotic value
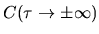 to be zero, to allow finite moments of
to be zero, to allow finite moments of 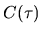 .
We will not restrict ourselves to phase-space-volume-preserving
deformations (i.e. ones which have
.
We will not restrict ourselves to phase-space-volume-preserving
deformations (i.e. ones which have 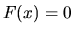 ).
).
The integral of (D.5) gives
the
general expression
![\begin{displaymath}
{\mathcal{G}}(t) \; = \; -m \int_0^t dt' \: \ddot{{\mathbf ...
...athbf a} + B{\mathbf r} + O(r^2) \cdots \right] \; - \; F(x)t.
\end{displaymath}](img1672.gif) |
(D.6) |
where the square brackets enclose the expansion of
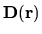 (each vector component is assumed to be a multi-dimensional
Taylor series about
(each vector component is assumed to be a multi-dimensional
Taylor series about
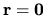 ), and
), and 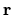 is
the position at time
is
the position at time 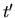 .
The coefficients
.
The coefficients
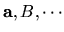 are rank
are rank  objects.
The linear growth rate
objects.
The linear growth rate 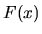 is determined uniquely for a given
is determined uniquely for a given  .
The linear growth (final term) is capable of cancelling deterministic linear
growth in the time-integral term; however, if the time-integral
grows diffusively, then no value of
.
The linear growth (final term) is capable of cancelling deterministic linear
growth in the time-integral term; however, if the time-integral
grows diffusively, then no value of 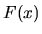 can prevent
can prevent
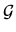 from being non-stationary.
Therefore a choice of
from being non-stationary.
Therefore a choice of
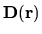 which is `special' will have
no terms in the time-integral which grow diffusively.
Note that, since
which is `special' will have
no terms in the time-integral which grow diffusively.
Note that, since
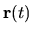 decorrelates on a timescale
of
decorrelates on a timescale
of
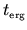 , diffusive growth (random walk) is the generic case.
, diffusive growth (random walk) is the generic case.
We treat the time-integral terms in (D.6) in increasing powers
of 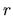 , (writing with Einstein summation notation):
, (writing with Einstein summation notation):
and so on.
What constraints arise on the coefficients for there to be no diffusive
growth terms?
The first result shows that since the integrand is an exact time derivative,
there is no diffusive growth for any 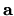 .
In general, any boundary-type terms (those
coming from exact time derivatives, shown with square brackets)
cannot cause diffusion since all functions of
.
In general, any boundary-type terms (those
coming from exact time derivatives, shown with square brackets)
cannot cause diffusion since all functions of
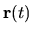 are stationary
and bounded (since the energy-surface is bounded in phase-space);
so these terms can be ignored.
The time-integral term in (D.8) will vanish if
are stationary
and bounded (since the energy-surface is bounded in phase-space);
so these terms can be ignored.
The time-integral term in (D.8) will vanish if 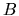 is
any antisymmetric tensor.
Any symmetric component in
is
any antisymmetric tensor.
Any symmetric component in 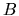 will give a quadratic form
in the momentum, and therefore a fluctuating function
whose time-integral grows diffusively.
The one important
exception to this is when this quadratic form is proportional
(up to an exact time derivative)
to
will give a quadratic form
in the momentum, and therefore a fluctuating function
whose time-integral grows diffusively.
The one important
exception to this is when this quadratic form is proportional
(up to an exact time derivative)
to 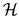 , the Hamiltonian.
, the Hamiltonian.
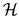 is a
constant of the motion, so gives uniform linear (non-diffusive)
growth of the time-integral.
This will correspond to the special nature of dilation in the hard-walled
case discussed in Sec. D.3.
is a
constant of the motion, so gives uniform linear (non-diffusive)
growth of the time-integral.
This will correspond to the special nature of dilation in the hard-walled
case discussed in Sec. D.3.
We can show that the higher terms (D.9), etc cause
diffusive growth, unless either all the coefficients
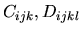 , etc
are zero, or unless the coefficients fall into the
`trivially special'
subspace corresponding to
, etc
are zero, or unless the coefficients fall into the
`trivially special'
subspace corresponding to
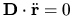 at all
accessible
at all
accessible 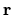 .
(This latter case imposes linear conditions on the coefficients;
we exclude the resulting deformation-less subspace).
For any given
.
(This latter case imposes linear conditions on the coefficients;
we exclude the resulting deformation-less subspace).
For any given 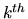 -order term, for instance (D.9) with
-order term, for instance (D.9) with 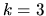 ,
the coefficient tensor must be totally symmetric with respect to
interchange of its last
,
the coefficient tensor must be totally symmetric with respect to
interchange of its last 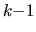 indices (nonsymmetric parts cancel
in the summation because of this symmetry in the
indices (nonsymmetric parts cancel
in the summation because of this symmetry in the 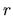 factors).
Note that this symmetry forbids the type of argument
that allowed an antisymmetric
factors).
Note that this symmetry forbids the type of argument
that allowed an antisymmetric 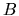 to give no diffusive growth for
to give no diffusive growth for 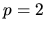 .
Manipulation
by parts conserves the symmetry of the
.
Manipulation
by parts conserves the symmetry of the 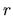 terms,
the power of
terms,
the power of 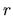 (namely
(namely 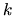 ), and the number
of time-derivatives, or `dots' (namely 2).
(It also generates ignorable boundary-type terms).
There are only two cases:
), and the number
of time-derivatives, or `dots' (namely 2).
(It also generates ignorable boundary-type terms).
There are only two cases:
- Both the dots are on the same
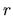 , in which case the integrand is
a (non-zero) function of position alone (since
, in which case the integrand is
a (non-zero) function of position alone (since 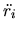 is a function
of position alone).
is a function
of position alone).
- The dots are on different
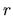 's, giving a quadratic form in
's, giving a quadratic form in 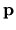 multiplied by a (non-zero)
function of
multiplied by a (non-zero)
function of 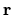 .
.
It is clear that by such manipulation, no exact time-derivative can be
produced.
The only other way to prevent diffusive growth is by
making the integrand a multiple of 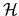 (plus exact time-
derivatives).
Case 2) cannot give the required
(plus exact time-
derivatives).
Case 2) cannot give the required 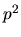 term so it is no help.
(The only
term so it is no help.
(The only 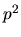 term can come from an isotropic
term can come from an isotropic 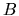 tensor).
It is unknown whether case 1) can give a term proportional
to
tensor).
It is unknown whether case 1) can give a term proportional
to
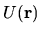 , which could add to an existing
, which could add to an existing 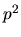 term to give
term to give 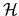 .
It seems this latter occurrence could only happen for particular forms
of
.
It seems this latter occurrence could only happen for particular forms
of
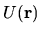 , for instance the scaling potentials given below
D.1.
If it happens, it would give a `dilation-type' special deformation
corresponding to conservation of
, for instance the scaling potentials given below
D.1.
If it happens, it would give a `dilation-type' special deformation
corresponding to conservation of 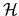 .
.
In conclusion this gives the form of a `special' deformation
(in a general potential) as
 |
(D.10) |
The first term accounts for
all possible translations, and the second all possible
rotations, in 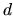 dimensions.
The existence of a `dilation-type' special deformation for
a general potential is still open.
dimensions.
The existence of a `dilation-type' special deformation for
a general potential is still open.



Next: Scaling potentials and the
Up: Appendix D: How Many
Previous: Requirement on time-integral of
Alex Barnett
2001-10-03
![]() must be defined everywhere in space
(note that it does not change in time).
The deformation parameter
must be defined everywhere in space
(note that it does not change in time).
The deformation parameter ![]() controls the hamiltonian
controls the hamiltonian
![]() , (writing with Einstein summation notation):
, (writing with Einstein summation notation):
![]() , etc
are zero, or unless the coefficients fall into the
`trivially special'
subspace corresponding to
, etc
are zero, or unless the coefficients fall into the
`trivially special'
subspace corresponding to
![]() at all
accessible
at all
accessible ![]() .
(This latter case imposes linear conditions on the coefficients;
we exclude the resulting deformation-less subspace).
For any given
.
(This latter case imposes linear conditions on the coefficients;
we exclude the resulting deformation-less subspace).
For any given ![]() -order term, for instance (D.9) with
-order term, for instance (D.9) with ![]() ,
the coefficient tensor must be totally symmetric with respect to
interchange of its last
,
the coefficient tensor must be totally symmetric with respect to
interchange of its last ![]() indices (nonsymmetric parts cancel
in the summation because of this symmetry in the
indices (nonsymmetric parts cancel
in the summation because of this symmetry in the ![]() factors).
Note that this symmetry forbids the type of argument
that allowed an antisymmetric
factors).
Note that this symmetry forbids the type of argument
that allowed an antisymmetric ![]() to give no diffusive growth for
to give no diffusive growth for ![]() .
Manipulation
by parts conserves the symmetry of the
.
Manipulation
by parts conserves the symmetry of the ![]() terms,
the power of
terms,
the power of ![]() (namely
(namely ![]() ), and the number
of time-derivatives, or `dots' (namely 2).
(It also generates ignorable boundary-type terms).
There are only two cases:
), and the number
of time-derivatives, or `dots' (namely 2).
(It also generates ignorable boundary-type terms).
There are only two cases:
![]() (plus exact time-
derivatives).
Case 2) cannot give the required
(plus exact time-
derivatives).
Case 2) cannot give the required ![]() term so it is no help.
(The only
term so it is no help.
(The only ![]() term can come from an isotropic
term can come from an isotropic ![]() tensor).
It is unknown whether case 1) can give a term proportional
to
tensor).
It is unknown whether case 1) can give a term proportional
to
![]() , which could add to an existing
, which could add to an existing ![]() term to give
term to give ![]() .
It seems this latter occurrence could only happen for particular forms
of
.
It seems this latter occurrence could only happen for particular forms
of
![]() , for instance the scaling potentials given below
D.1.
If it happens, it would give a `dilation-type' special deformation
corresponding to conservation of
, for instance the scaling potentials given below
D.1.
If it happens, it would give a `dilation-type' special deformation
corresponding to conservation of ![]() .
.