


Next: `Automatic' normalisation of states
Up: Higher-order correction and normalization
Previous: Higher-order correction and normalization
In Fig. 6.4 (bottom) the consistent curvature in the predicted
shifts 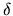 implies that higher-order effects could be important
in predicting the
implies that higher-order effects could be important
in predicting the 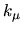 values.
There are many levels of higher-order correction possible
once the basic diagonalization of (6.25) has been performed:
1) identification of the higher-order diagonal terms in
values.
There are many levels of higher-order correction possible
once the basic diagonalization of (6.25) has been performed:
1) identification of the higher-order diagonal terms in 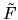 and
and 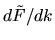 for an average state, then correcting all the
for an average state, then correcting all the 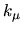 according to the same resulting formula,
2) using
according to the same resulting formula,
2) using
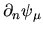 for each state on the boundary to
compute a correction for each corresponding
for each state on the boundary to
compute a correction for each corresponding 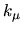 ,
3) using
,
3) using
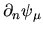 for each state on the boundary and knowledge of
off-diagonal terms in
for each state on the boundary and knowledge of
off-diagonal terms in 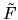 and
and 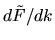 to compute
corrections to the eigenvectors
to compute
corrections to the eigenvectors
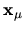 as well as the
as well as the 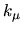 .
I will only report on the first of these ideas, since it is easiest to
routinely implement.
The other two levels of correction are areas for investigation, however
it is not known whether they will prove even worthwhile (there
is a trade-off betweeen correcting the results of one diagonalization and
simply performing more diagonalizations).
My inkling is that in practice
the corrections presented here will be the only worthwhile ones.
.
I will only report on the first of these ideas, since it is easiest to
routinely implement.
The other two levels of correction are areas for investigation, however
it is not known whether they will prove even worthwhile (there
is a trade-off betweeen correcting the results of one diagonalization and
simply performing more diagonalizations).
My inkling is that in practice
the corrections presented here will be the only worthwhile ones.
Appendix I shows that the expansion of the diagonal of the
tension matrix is
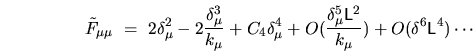 |
(6.27) |
where the coefficient 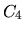 is the sum of many complicated boundary integrals
of
is the sum of many complicated boundary integrals
of
 ,
,
 , etc, and
the local curvature
, etc, and
the local curvature 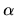 and its derivative.
It is possible in theory to perform a random-wave estimate for these integrals
to reach an expression in terms of the billiard shape.
However in practice it is much easier to fit for
and its derivative.
It is possible in theory to perform a random-wave estimate for these integrals
to reach an expression in terms of the billiard shape.
However in practice it is much easier to fit for 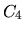 by measuring the
average value for
a few states.
For instance, in the quarter stadium of length 2 by height 1,
by measuring the
average value for
a few states.
For instance, in the quarter stadium of length 2 by height 1,
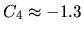 .
However, it varies from state to state
6.3,
taking smaller values for states with higher average transverse momentum on the
boundary, or for states which are scarred so as to avoid regions of high
.
However, it varies from state to state
6.3,
taking smaller values for states with higher average transverse momentum on the
boundary, or for states which are scarred so as to avoid regions of high
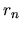 .
Note that
.
Note that 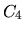 has units of length squared, so that if the billiard changes
size, then
has units of length squared, so that if the billiard changes
size, then 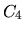 will need to be scaled accordingly.
will need to be scaled accordingly.
The generalized eigenvalue is
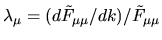 which can be
found from (6.27). Inversion of the series expansion
is needed to get the series for our estimate for
which can be
found from (6.27). Inversion of the series expansion
is needed to get the series for our estimate for 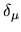 , giving
, giving
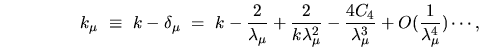 |
(6.28) |
where corrections of
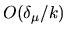 have been ignored. This is our
improved version of (6.26).
In tests, use of this formula had little effect on the
have been ignored. This is our
improved version of (6.26).
In tests, use of this formula had little effect on the 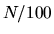 most accurate states, but the resulting wavenumber shift reduced the
tension of the remainder of the
useful states by a factor of
most accurate states, but the resulting wavenumber shift reduced the
tension of the remainder of the
useful states by a factor of 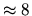 (see Fig. 6.9).
Also, the
(see Fig. 6.9).
Also, the
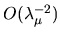 term had very little effect (much less
than the
term had very little effect (much less
than the
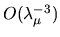 ) because
of the
) because
of the 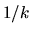 factor.
The utility of higher-order expansion is minimal (the next significant, the
sixth-order, has little effect).
factor.
The utility of higher-order expansion is minimal (the next significant, the
sixth-order, has little effect).
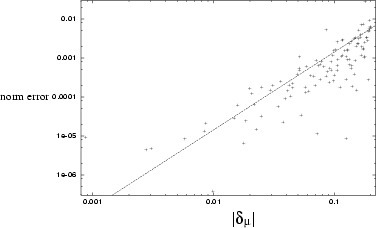
Figure 6.8:
Automatic normalization of states returned by the scaling method at
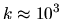 , using (6.29). The error from 1 is shown.
The growth of random norm errors roughly follows a second power law
(shown by the staight line).
, using (6.29). The error from 1 is shown.
The growth of random norm errors roughly follows a second power law
(shown by the staight line).
 |



Next: `Automatic' normalisation of states
Up: Higher-order correction and normalization
Previous: Higher-order correction and normalization
Alex Barnett
2001-10-03
![]() implies that higher-order effects could be important
in predicting the
implies that higher-order effects could be important
in predicting the ![]() values.
There are many levels of higher-order correction possible
once the basic diagonalization of (6.25) has been performed:
1) identification of the higher-order diagonal terms in
values.
There are many levels of higher-order correction possible
once the basic diagonalization of (6.25) has been performed:
1) identification of the higher-order diagonal terms in ![]() and
and ![]() for an average state, then correcting all the
for an average state, then correcting all the ![]() according to the same resulting formula,
2) using
according to the same resulting formula,
2) using
![]() for each state on the boundary to
compute a correction for each corresponding
for each state on the boundary to
compute a correction for each corresponding ![]() ,
3) using
,
3) using
![]() for each state on the boundary and knowledge of
off-diagonal terms in
for each state on the boundary and knowledge of
off-diagonal terms in ![]() and
and ![]() to compute
corrections to the eigenvectors
to compute
corrections to the eigenvectors
![]() as well as the
as well as the ![]() .
I will only report on the first of these ideas, since it is easiest to
routinely implement.
The other two levels of correction are areas for investigation, however
it is not known whether they will prove even worthwhile (there
is a trade-off betweeen correcting the results of one diagonalization and
simply performing more diagonalizations).
My inkling is that in practice
the corrections presented here will be the only worthwhile ones.
.
I will only report on the first of these ideas, since it is easiest to
routinely implement.
The other two levels of correction are areas for investigation, however
it is not known whether they will prove even worthwhile (there
is a trade-off betweeen correcting the results of one diagonalization and
simply performing more diagonalizations).
My inkling is that in practice
the corrections presented here will be the only worthwhile ones.
![]() which can be
found from (6.27). Inversion of the series expansion
is needed to get the series for our estimate for
which can be
found from (6.27). Inversion of the series expansion
is needed to get the series for our estimate for ![]() , giving
, giving
