


Next: Appendix F: Cross correlations
Up: Dissipation in Deforming Chaotic
Previous: Scaling potentials and the
Appendix E: Cross correlations I: general-special
Consider two noisy signals
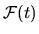 and
and
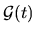 .
We assume that
.
We assume that
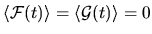 .
The angular brackets stand for an average over realizations.
The auto-correlations of
.
The angular brackets stand for an average over realizations.
The auto-correlations of
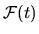 and
and
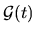 are described by functions
are described by functions
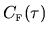 and
and
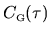 respectively. We assume that both
auto-correlation functions are short-range, meaning
no power-law tails (this corresponds to the hard chaos
assumption of this paper),
and that they are negligible beyond a time
respectively. We assume that both
auto-correlation functions are short-range, meaning
no power-law tails (this corresponds to the hard chaos
assumption of this paper),
and that they are negligible beyond a time
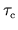 .
We call a signal `special' if the algebraic area under its auto-correlation
is zero.
The cross-correlation function is defined as
.
We call a signal `special' if the algebraic area under its auto-correlation
is zero.
The cross-correlation function is defined as
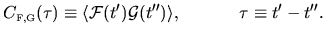 |
|
|
(E.1) |
We assume stationary processes so that the cross-correlation
function depends only on the time difference 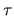 .
We also symmetrize this function if it does not have
.
We also symmetrize this function if it does not have
 symmetry. We assume that
symmetry. We assume that
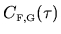 is short-range, meaning that it becomes negligibly small
for
is short-range, meaning that it becomes negligibly small
for
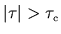 .
We would like to prove that if either
.
We would like to prove that if either
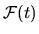 or
or
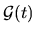 is special
then the algebraic area under the cross-correlation
function equals zero.
is special
then the algebraic area under the cross-correlation
function equals zero.
Consider the case where
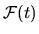 is general
while
is general
while
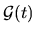 is special.
The integral of
is special.
The integral of
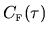 will be
denoted by
will be
denoted by 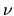 .
Define the processes
.
Define the processes
From our assumptions it follows, disregarding
a transient, that for
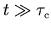 we have
diffusive growth
we have
diffusive growth
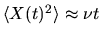 .
(It may help the reader to review the discussion in Section 2.1.6).
However since
.
(It may help the reader to review the discussion in Section 2.1.6).
However since 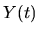 is a stationary process [79],
is a stationary process [79],
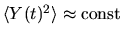 .
Therefore for a typical realization we have
.
Therefore for a typical realization we have
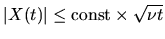 and
and
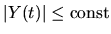 . Consequently, without
making any claims on the independence of
. Consequently, without
making any claims on the independence of 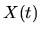 and
and 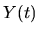 ,
we get that
,
we get that
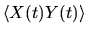 cannot grow
faster than
cannot grow
faster than
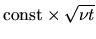 .
Using the definitions (E.2), (E.3)
and (E.1) we can write
.
Using the definitions (E.2), (E.3)
and (E.1) we can write
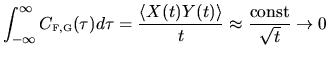 |
|
|
(E.4) |
where the limit
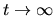 is taken.
Thus we have proved our assertion.
is taken.
Thus we have proved our assertion.



Next: Appendix F: Cross correlations
Up: Dissipation in Deforming Chaotic
Previous: Scaling potentials and the
Alex Barnett
2001-10-03
![]() and
and
![]() .
We assume that
.
We assume that
![]() .
The angular brackets stand for an average over realizations.
The auto-correlations of
.
The angular brackets stand for an average over realizations.
The auto-correlations of
![]() and
and
![]() are described by functions
are described by functions
![]() and
and
![]() respectively. We assume that both
auto-correlation functions are short-range, meaning
no power-law tails (this corresponds to the hard chaos
assumption of this paper),
and that they are negligible beyond a time
respectively. We assume that both
auto-correlation functions are short-range, meaning
no power-law tails (this corresponds to the hard chaos
assumption of this paper),
and that they are negligible beyond a time
![]() .
We call a signal `special' if the algebraic area under its auto-correlation
is zero.
The cross-correlation function is defined as
.
We call a signal `special' if the algebraic area under its auto-correlation
is zero.
The cross-correlation function is defined as
![]() is general
while
is general
while
![]() is special.
The integral of
is special.
The integral of
![]() will be
denoted by
will be
denoted by ![]() .
Define the processes
.
Define the processes