


Next: Volume integrals of vector
Up: Matrix trick for pushing
Previous: Matrix trick for pushing
Volume integrals of scalar quantities
By taking the divergence of all the types of terms appearing in relevant
vector identities, the following matrix relation is reached,
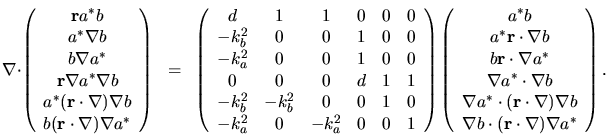 |
(H.10) |
The scalar coefficient matrix is formed by finding
the linear amounts of each of the 6 scalar functions which result
from performing the divergences on each vector term.
Deducing a few of the entries requires Einstein summation form,
and substitution of the Helmholtz equation, but all are simple.
It is convenient that 6 inputs gives 6 outputs since the matrix is
then possibly invertible. Its determinant is found to be
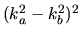 ,
implying that it is invertible for
,
implying that it is invertible for 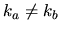 .
The relation (H.10) can be written
.
The relation (H.10) can be written
 |
(H.11) |
where the sum over 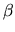 is implied. Care should be taken not to
confuse spatial coordinates (boldface vectors) with coefficient
indices
is implied. Care should be taken not to
confuse spatial coordinates (boldface vectors) with coefficient
indices
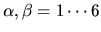 (Greek letters).
Integrating over the domain
(Greek letters).
Integrating over the domain 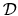 , applying Gauss' theorem and
premultiplying by the inverse of
, applying Gauss' theorem and
premultiplying by the inverse of 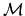 gives
gives
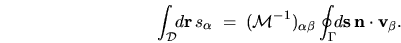 |
(H.12) |
Thus we have closed-form expressions for the volume integrals of any of the
6 scalar functions, in terms of boundary integrals.
That is, we have `pushed' the problem onto the boundary, as desired.
The symbolic inverse can be found
(e.g. using the Mathematica software package),
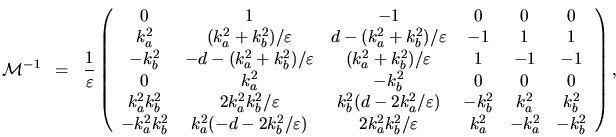 |
(H.13) |
where
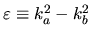 is the `energy difference'.
Rows of this matrix give the desired expressions for volume integrals.
For instance, (H.5) results from row 1.
is the `energy difference'.
Rows of this matrix give the desired expressions for volume integrals.
For instance, (H.5) results from row 1.
When 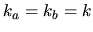 rows 2 and 3 of
rows 2 and 3 of 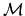 become identical, so the matrix is
singular and the above inversion fails.
However, it is still possible to extract solutions to this singular
problem by finding a vector
become identical, so the matrix is
singular and the above inversion fails.
However, it is still possible to extract solutions to this singular
problem by finding a vector 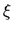 such that
such that
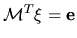 for a desired unit vector
for a desired unit vector 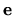 .
This is only possible if the unit vector lies entirely
within the row space
of
.
This is only possible if the unit vector lies entirely
within the row space
of 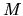 [188].
For instance, the first unit vector
[188].
For instance, the first unit vector
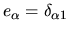 gives
gives
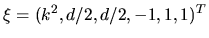 ,
corresponding to
,
corresponding to
This is a manifestly symmetric form of (H.7).
Its derivation is much more routine than that of Boasman[33] because
the matrix method automatically handles the coefficients.



Next: Volume integrals of vector
Up: Matrix trick for pushing
Previous: Matrix trick for pushing
Alex Barnett
2001-10-03
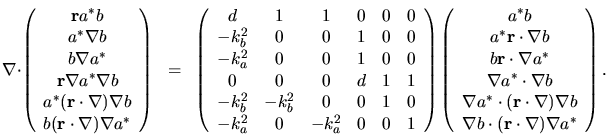
![]() rows 2 and 3 of
rows 2 and 3 of ![]() become identical, so the matrix is
singular and the above inversion fails.
However, it is still possible to extract solutions to this singular
problem by finding a vector
become identical, so the matrix is
singular and the above inversion fails.
However, it is still possible to extract solutions to this singular
problem by finding a vector ![]() such that
such that
![]() for a desired unit vector
for a desired unit vector ![]() .
This is only possible if the unit vector lies entirely
within the row space
of
.
This is only possible if the unit vector lies entirely
within the row space
of ![]() [188].
For instance, the first unit vector
[188].
For instance, the first unit vector
![]() gives
gives
![]() ,
corresponding to
,
corresponding to