


Next: Appendix I: Scaling expansion
Up: Other matrix elements
Previous: Dipole matrix elements:
For 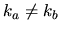 we have for the differential dilation operator,
we have for the differential dilation operator,
where again
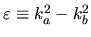 .
This follows from row 2 of the matrix
.
This follows from row 2 of the matrix
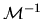 .
In the Dirichlet BC case this becomes,
.
In the Dirichlet BC case this becomes,
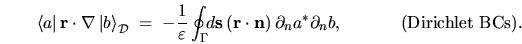 |
(H.25) |
The integral is proportional to the matrix element
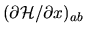 of the billiard dilation deformation.
of the billiard dilation deformation.
No general form for 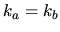 has been found. The
corresponding unit vector
has been found. The
corresponding unit vector
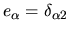 does not lie in
the row space of
does not lie in
the row space of
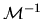 , indicating that other boundary
derivatives are needed as input.
However, for the particular case of Dirichlet BCs and
, indicating that other boundary
derivatives are needed as input.
However, for the particular case of Dirichlet BCs and 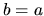 there exists the
simple formula
there exists the
simple formula
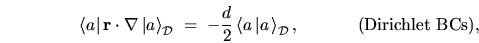 |
(H.26) |
which can be derived by expanding
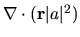 and integrating
over the domain.
and integrating
over the domain.



Next: Appendix I: Scaling expansion
Up: Other matrix elements
Previous: Dipole matrix elements:
Alex Barnett
2001-10-03
![]() we have for the differential dilation operator,
we have for the differential dilation operator,
![]() has been found. The
corresponding unit vector
has been found. The
corresponding unit vector
![]() does not lie in
the row space of
does not lie in
the row space of
![]() , indicating that other boundary
derivatives are needed as input.
However, for the particular case of Dirichlet BCs and
, indicating that other boundary
derivatives are needed as input.
However, for the particular case of Dirichlet BCs and ![]() there exists the
simple formula
there exists the
simple formula