


Next: Differential dilation matrix elements:
Up: Other matrix elements
Previous: Momentum matrix elements:
For 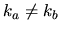 we have for each component
we have for each component 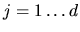 of the dipole (position) operator,
of the dipole (position) operator,
where as before
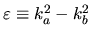 .
This follows from row 3 of the matrix
.
This follows from row 3 of the matrix
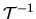 .
Summation over
.
Summation over 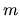 is implied. A mixture of vector and Einstein notations has
been avoided.
In the Dirichlet BC case this becomes
is implied. A mixture of vector and Einstein notations has
been avoided.
In the Dirichlet BC case this becomes
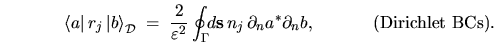 |
(H.23) |
Note that the integral is proportional to the matrix element
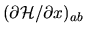 of the billiard deformation corresponding to translation in the
of the billiard deformation corresponding to translation in the 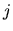 direction.
direction.
No form for 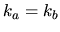 has been found.
The corresponding unit vector
has been found.
The corresponding unit vector
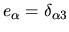 does not lie in
the row space of
does not lie in
the row space of
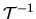 , indicating that other boundary
derivatives are needed as input.
, indicating that other boundary
derivatives are needed as input.
Alex Barnett
2001-10-03
![]() we have for each component
we have for each component ![]() of the dipole (position) operator,
of the dipole (position) operator,
![]() has been found.
The corresponding unit vector
has been found.
The corresponding unit vector
![]() does not lie in
the row space of
does not lie in
the row space of
![]() , indicating that other boundary
derivatives are needed as input.
, indicating that other boundary
derivatives are needed as input.