


Next: Dipole matrix elements:
Up: Other matrix elements
Previous: Other matrix elements
For 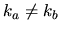 we have for each component
we have for each component 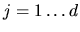 of the grad operator,
of the grad operator,
![\begin{displaymath}
\left\langle a\right\vert\partial_j\left\vert b\right\rangl...
...k_a^2 a^* b - (\partial_m a^*) \partial_m b \right] \right\} .
\end{displaymath}](img1854.gif) |
(H.20) |
This follows from row 1 of the matrix
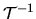 .
Summation over
.
Summation over 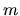 is implied.
is implied.
For 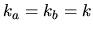 it is unambiguous to write all components
together as a vector relation thus,
it is unambiguous to write all components
together as a vector relation thus,
![\begin{displaymath}
\left\langle a\right\vert\nabla\left\vert b\right\rangle _{...
...+ {\mathbf r} (a^* \partial_n b - b \partial_n a^* ) \right ].
\end{displaymath}](img1856.gif) |
(H.21) |
This follows from the singular solution
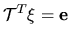 for the first unit vector
for the first unit vector 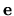 .
It is interesting that the equal wavenumber case involves one order
of derivative less than the unequal case.
In the Dirichlet BC case, (H.21) vanishes.
.
It is interesting that the equal wavenumber case involves one order
of derivative less than the unequal case.
In the Dirichlet BC case, (H.21) vanishes.
Alex Barnett
2001-10-03
![]() we have for each component
we have for each component ![]() of the grad operator,
of the grad operator,
![]() it is unambiguous to write all components
together as a vector relation thus,
it is unambiguous to write all components
together as a vector relation thus,