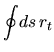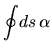Next: Appendix J: Helmholtz basis
Up: Appendix I: Scaling expansion
Previous: Tension matrix expansion
Here I give a couple of geometrical results in billiards
which found no other place to hide.
In arbitrary  we have
we have
 |
(I.24) |
where as usual 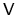 is the billiard volume.
For
is the billiard volume.
For 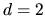 we have
we have
where the local curvature 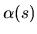 is defined in Section I.2.
is defined in Section I.2.
Alex Barnett
2001-10-03
![]() we have
we have