In this appendix we derive the transmission cross-section
of the idealised slit from Section 7.3, in the
tunneling limit ![]() .
We first consider a simple scaling argument which gives the dependence on
.
We first consider a simple scaling argument which gives the dependence on
![]() and
and ![]() , and then find the correct prefactor.
, and then find the correct prefactor.
The slit system possesses a scaling property (shared by all hard-walled
quantum systems):
it is invariant under a rescaling of space
![]() provided there is a corresponding rescaling of wavevector
provided there is a corresponding rescaling of wavevector
![]() .
Our slit potential is defined by a single parameter
.
Our slit potential is defined by a single parameter ![]() , the slit
half-width.
The particle wavelength
, the slit
half-width.
The particle wavelength
![]() is the only other length scale in the problem.
This means that for a given incident wave,
the form of the full scattering wavefunction,
and hence the ratio of the quantum to classical transmission cross-sections,
can only depend on
is the only other length scale in the problem.
This means that for a given incident wave,
the form of the full scattering wavefunction,
and hence the ratio of the quantum to classical transmission cross-sections,
can only depend on ![]() .
(In other words, if the wavelength changes in proportion to the slit size,
we are viewing the original problem with a new unit of length.)
The classical cross-section is proportional to
.
(In other words, if the wavelength changes in proportion to the slit size,
we are viewing the original problem with a new unit of length.)
The classical cross-section is proportional to ![]() .
Therefore the quantum cross-section must have the exact form
.
Therefore the quantum cross-section must have the exact form
We seek ![]() in the
in the ![]() limit.
For a hard-walled system solutions of Schrodinger's equation become
those of the Helmholtz equation with Dirichlet boundary conditions.
Close to the slit (a distance
limit.
For a hard-walled system solutions of Schrodinger's equation become
those of the Helmholtz equation with Dirichlet boundary conditions.
Close to the slit (a distance ![]() )
they become
well approximated
by the
)
they become
well approximated
by the ![]() limit, namely solutions of Laplace's equation.
Thus we can use `electrostatics' at these small distances,
and then match to the small-
limit, namely solutions of Laplace's equation.
Thus we can use `electrostatics' at these small distances,
and then match to the small-![]() tails of the
Helmholtz solutions to find the transmitted flux.
The solutions obtained in this way have been known for over a century,
and were first found by Lord Rayleigh ([168]
in which the scattering solutions are derived for
tails of the
Helmholtz solutions to find the transmitted flux.
The solutions obtained in this way have been known for over a century,
and were first found by Lord Rayleigh ([168]
in which the scattering solutions are derived for ![]() Dirichlet
and Neumann apertures
and their inverses, in both 2D and 3D.
See p. 270-1 for our particular case).
The transmission is dominated by scattering of incoming dipole (
Dirichlet
and Neumann apertures
and their inverses, in both 2D and 3D.
See p. 270-1 for our particular case).
The transmission is dominated by scattering of incoming dipole (![]() )
radiation to outgoing dipole radiation; we will justify
this shortly.
)
radiation to outgoing dipole radiation; we will justify
this shortly.
The dipole parts of the 2D Laplace solution can be written generally as
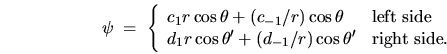 |
(K.2) |
The dimensional scaling of (K.3) implies ![]() ,
so at constant
,
so at constant ![]() the transmitted flux, and hence
the transmitted flux, and hence
![]() , grows like
, grows like ![]() .
Comparison with (K.1) immediately gives
the scaling
.
Comparison with (K.1) immediately gives
the scaling
![]() .
This
.
This ![]() dependence of cross section for a given aperture size is
the 2D equivalent of Rayleigh's famous
dependence of cross section for a given aperture size is
the 2D equivalent of Rayleigh's famous ![]() law for dipole light scattering in 3D explaining why the sky
appears blue [167] (see also [105] p.418).
law for dipole light scattering in 3D explaining why the sky
appears blue [167] (see also [105] p.418).
How does the contribution of higher multipole radiation scale?
The exact Laplace solution with general asymptotic form
will involve generalizing
Eq.(K.3) to a linear matrix relation connecting all the
![]() and
and ![]() with
with
![]() to all those
with
to all those
with
![]() .
However because of the associated
.
However because of the associated ![]() and
and ![]() factors,
by dimensional arguments
all the elements of this matrix (other than the
factors,
by dimensional arguments
all the elements of this matrix (other than the ![]() already considered
above)
will scale like
powers of
already considered
above)
will scale like
powers of ![]() higher than 2.
It is important to realise that the Laplace coefficients
higher than 2.
It is important to realise that the Laplace coefficients
![]() (
(![]() ) directly connect to the respective
coefficients of Bessel functions of
) directly connect to the respective
coefficients of Bessel functions of ![]() type for
type for ![]() and
and
![]() type for
type for ![]() on the left (right) sides, which
in turn determine the incoming and outgoing waves of angular
momentum
on the left (right) sides, which
in turn determine the incoming and outgoing waves of angular
momentum ![]() on those same sides.
Therefore the resulting contribution to
on those same sides.
Therefore the resulting contribution to
![]() due to
excitation by the
due to
excitation by the ![]() channel on the left and re-radiation into the
channel on the left and re-radiation into the
![]() channel on the right
will scale as
channel on the right
will scale as ![]() .
This contribution
will therefore be smaller than the dipole-dipole
(
.
This contribution
will therefore be smaller than the dipole-dipole
(![]() ,
, ![]() ) component by a factor
) component by a factor
![]() .
In fact, because of symmetry about the
.
In fact, because of symmetry about the ![]() -axis, the
system only couples even
-axis, the
system only couples even ![]() to even
to even ![]() and odd
and odd ![]() to odd
to odd ![]() ;
this guarantees that the most significant correction
is in fact a factor
;
this guarantees that the most significant correction
is in fact a factor ![]() down.
Thus in our
down.
Thus in our ![]() limit we are justified
in using only p-wave scattering: dipole `absorption' from
limit we are justified
in using only p-wave scattering: dipole `absorption' from
![]() ,
and dipole re-radiation into
,
and dipole re-radiation into
![]() .
(There will also be equal dipole re-radiation into
.
(There will also be equal dipole re-radiation into
![]() ,
which interferes with
,
which interferes with
![]() but does not affect the conductance).
but does not affect the conductance).
We now can find the prefactor.
The connection between the Laplace dipole solution (![]() )
and the outgoing
dipole coefficient
)
and the outgoing
dipole coefficient ![]() (see Section 7.2)
is found by matching to the small-
(see Section 7.2)
is found by matching to the small-![]() form
[7] of the Neumann part
form
[7] of the Neumann part ![]() of the Hankel function.
This gives
of the Hankel function.
This gives
![]() .
Combining this with (K.3) and the correct Laplace slit result
.
Combining this with (K.3) and the correct Laplace slit result
![]() [168,148]
gives
[168,148]
gives
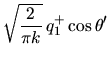 |
|||
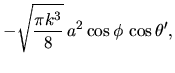 |
(K.5) |
Note that
![]() is equal to
is equal to
![]() , because
the reflected dipole strength is equal to the transmitted.
(The dipole is also `two-headed', radiating in phase on both sides).
, because
the reflected dipole strength is equal to the transmitted.
(The dipole is also `two-headed', radiating in phase on both sides).
It is interesting to note that in any hard-walled
scattering system,
the conductance can only be a function of the product ![]() .
This follows from substitution of Eq.(K.1)
into Eq.(7.12).
.
This follows from substitution of Eq.(K.1)
into Eq.(7.12).