


Next: Historical remarks and conclusion
Up: Beyond the WNA
Previous: Beyond the WNA
In Fig. 4.8
we use the IFIF to estimate 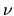 for two examples.
The first is a deformation (CO + W16) whose normal component
is `good', due its oscillatory nature. The deviation
from a flat white power spectrum is
for two examples.
The first is a deformation (CO + W16) whose normal component
is `good', due its oscillatory nature. The deviation
from a flat white power spectrum is 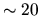 % for the
normal component.
The IFIF result Eq.(4.11) is accurate to a few percent.
It is a much better estimate of the actual
% for the
normal component.
The IFIF result Eq.(4.11) is accurate to a few percent.
It is a much better estimate of the actual 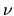 compared
with the naive WNA Eq.(3.12) which overestimates
the correct value by a factor of 2.2.
In the second example the deformation is SX.
The resulting normal component is `bad'. Its
power spectrum fluctuates by a factor of about 10
in the
compared
with the naive WNA Eq.(3.12) which overestimates
the correct value by a factor of 2.2.
In the second example the deformation is SX.
The resulting normal component is `bad'. Its
power spectrum fluctuates by a factor of about 10
in the 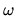 range shown.
Consequently the IFIF
is limited in its accuracy, and the correct value
for
range shown.
Consequently the IFIF
is limited in its accuracy, and the correct value
for 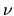 is underestimated by a factor of 2.5.
However, it is still a great improvement over the
naive result Eq.(3.12).
In this second example we can extract another prediction
about
is underestimated by a factor of 2.5.
However, it is still a great improvement over the
naive result Eq.(3.12).
In this second example we can extract another prediction
about
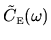 . The special component is a factor
. The special component is a factor 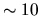 larger
than the normal component. Therefore
the
larger
than the normal component. Therefore
the 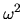 behavior at small
behavior at small 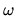 is almost entirely
due to the `rotation' component. The prefactor of the
is almost entirely
due to the `rotation' component. The prefactor of the
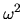 behavior need only be found once for each billiard shape.
This saves computation and
gives an extra information about the dissipation rate
at finite driving frequency.
behavior need only be found once for each billiard shape.
This saves computation and
gives an extra information about the dissipation rate
at finite driving frequency.
Figure 4.7:
a) A deformation of the stadium which moves the
`center of mass' (centroid) of the cavity to the right
(from the dot to the crosshairs symbol).
This deformation is orthogonal
(in the sense of (4.5))
to all special deformations,
in particular, all translations.
b) An example volume-preserving deformation of an elongated
approximately-rectangular
cavity (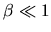 ) which nevertheless has a large overlap
with dilation.
It can be shown that this results in an IFIF
estimate of
) which nevertheless has a large overlap
with dilation.
It can be shown that this results in an IFIF
estimate of
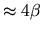 times
that of the naive WNA.
In both diagrams the undeformed shape is shown as a heavy line,
the deformed one as a thin line.
times
that of the naive WNA.
In both diagrams the undeformed shape is shown as a heavy line,
the deformed one as a thin line.
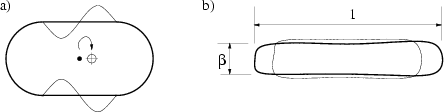 |
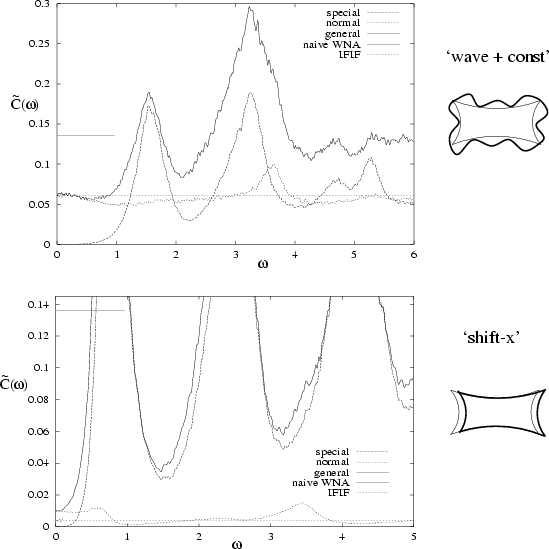
Figure 4.8:
Decomposition of general deformations 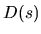 into
orthogonal `normal' and `special' components.
The general deformation is CO + W16 in subfigure (a),
and SX in subfigure (b).
The naive WNA Eq.(3.12) is indicated by short solid line.
The improved (IFIF) result Eq.(4.11) is indicated by long dashed arrow.
In (a) the normal component is quite `good', giving an accurate
IFIF result, but in (b) the normal component of SX is `bad',
limiting the accuracy of the IFIF to 40% of the actual
into
orthogonal `normal' and `special' components.
The general deformation is CO + W16 in subfigure (a),
and SX in subfigure (b).
The naive WNA Eq.(3.12) is indicated by short solid line.
The improved (IFIF) result Eq.(4.11) is indicated by long dashed arrow.
In (a) the normal component is quite `good', giving an accurate
IFIF result, but in (b) the normal component of SX is `bad',
limiting the accuracy of the IFIF to 40% of the actual 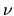 .
.
 |



Next: Historical remarks and conclusion
Up: Beyond the WNA
Previous: Beyond the WNA
Alex Barnett
2001-10-03
![]() for two examples.
The first is a deformation (CO + W16) whose normal component
is `good', due its oscillatory nature. The deviation
from a flat white power spectrum is
for two examples.
The first is a deformation (CO + W16) whose normal component
is `good', due its oscillatory nature. The deviation
from a flat white power spectrum is ![]() % for the
normal component.
The IFIF result Eq.(4.11) is accurate to a few percent.
It is a much better estimate of the actual
% for the
normal component.
The IFIF result Eq.(4.11) is accurate to a few percent.
It is a much better estimate of the actual ![]() compared
with the naive WNA Eq.(3.12) which overestimates
the correct value by a factor of 2.2.
In the second example the deformation is SX.
The resulting normal component is `bad'. Its
power spectrum fluctuates by a factor of about 10
in the
compared
with the naive WNA Eq.(3.12) which overestimates
the correct value by a factor of 2.2.
In the second example the deformation is SX.
The resulting normal component is `bad'. Its
power spectrum fluctuates by a factor of about 10
in the ![]() range shown.
Consequently the IFIF
is limited in its accuracy, and the correct value
for
range shown.
Consequently the IFIF
is limited in its accuracy, and the correct value
for ![]() is underestimated by a factor of 2.5.
However, it is still a great improvement over the
naive result Eq.(3.12).
In this second example we can extract another prediction
about
is underestimated by a factor of 2.5.
However, it is still a great improvement over the
naive result Eq.(3.12).
In this second example we can extract another prediction
about
![]() . The special component is a factor
. The special component is a factor ![]() larger
than the normal component. Therefore
the
larger
than the normal component. Therefore
the ![]() behavior at small
behavior at small ![]() is almost entirely
due to the `rotation' component. The prefactor of the
is almost entirely
due to the `rotation' component. The prefactor of the
![]() behavior need only be found once for each billiard shape.
This saves computation and
gives an extra information about the dissipation rate
at finite driving frequency.
behavior need only be found once for each billiard shape.
This saves computation and
gives an extra information about the dissipation rate
at finite driving frequency.

