


Next: Quasi-orthogonality on the boundary
Up: The basic scaling method
Previous: The basic scaling method
Tension matrix in a scaling eigenfunction basis
It is important to define a spatial rescaling of a wavefunction,
corresponding to dilation (or contraction) about the (arbitrary) origin.
If the wavefunction
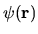 is a Helmholtz solution at wavenumber
is a Helmholtz solution at wavenumber 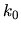 ,
then the rescaled version
,
then the rescaled version
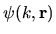 of the same wavefunction
obeys the Helmholtz equation at a new wavenumber
of the same wavefunction
obeys the Helmholtz equation at a new wavenumber 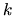 :
:
 |
(6.1) |
The rescaled function value at a given point is found by looking at the
original function at a point a fractional distance 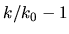 further from the origin.
The derivative with respect to
further from the origin.
The derivative with respect to 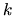 of the wavefunction value at a point
of the wavefunction value at a point
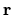 is
is
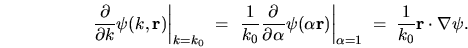 |
(6.2) |
This means that for 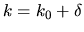 with
with 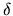 small (
small (
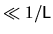 ), this
can be expanded in powers of
), this
can be expanded in powers of 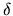 as
as
![\begin{displaymath}
\psi(k_0 + \delta,{\mathbf r}) \; = \; \left[ 1 + \frac{\de...
...dot\nabla + O(\delta^2) \cdots \right] \, \psi{({\mathbf r})}.
\end{displaymath}](img864.gif) |
(6.3) |
We will not need any higher terms for the basic method (they are given in
Appendix I).
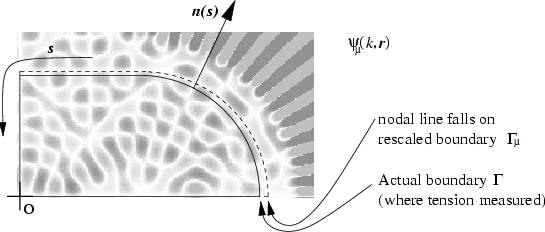
Figure:
Scaling eigenfunction
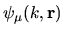 vanishes on a rescaled boundary
vanishes on a rescaled boundary
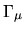 .
It is clear that when
.
It is clear that when  is much closer than a wavelength from
is much closer than a wavelength from  ,
the wavefunction can be linearized,
giving a value on
,
the wavefunction can be linearized,
giving a value on 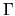 proportional to the eigenfunction normal derivative.
Also the boundary coordinate
proportional to the eigenfunction normal derivative.
Also the boundary coordinate 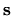 and local surface normal
and local surface normal
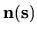 are shown.
are shown.
 |
We now choose a basis
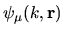 of the exact billiard eigenfunctions scaled as above to have
a single wavenumber
of the exact billiard eigenfunctions scaled as above to have
a single wavenumber 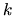 ; these are called scaling eigenfunctions [195].
The unscaled eigenfunctions are taken to have unit normalization
in the billiard.
The index
; these are called scaling eigenfunctions [195].
The unscaled eigenfunctions are taken to have unit normalization
in the billiard.
The index
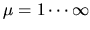 labels the eigenfunctions in ascending order of
their unscaled wavenumber
labels the eigenfunctions in ascending order of
their unscaled wavenumber 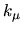 .
The scaling eigenfunctions no longer go to zero on the original billiard
boundary
.
The scaling eigenfunctions no longer go to zero on the original billiard
boundary 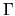 , however they do go to zero on rescaled (dilated
or contracted) versions
of the boundary
, however they do go to zero on rescaled (dilated
or contracted) versions
of the boundary 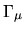 (see Fig. 6.1).
Imagine that a state
(see Fig. 6.1).
Imagine that a state 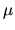 has a wavenumber shift
has a wavenumber shift
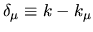 which is very small (
which is very small (
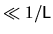 , the inverse system size).
Then
, the inverse system size).
Then 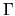 will be very close to
will be very close to 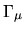 , and the value of
, and the value of
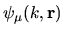 for
for
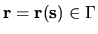 will
be close to zero.
The boundary coordinate
will
be close to zero.
The boundary coordinate 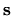 measures location on
measures location on 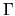 .
Applying (6.3), the difference from zero is given by
.
Applying (6.3), the difference from zero is given by
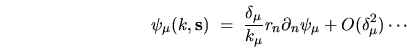 |
(6.4) |
where
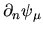 is the (unscaled) eigenstate normal derivative
at location
is the (unscaled) eigenstate normal derivative
at location 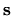 .
Notice that the zeroth-order term vanished because of the BCs.
(This expansion is continued in Appendix I).
A general sum of scaling eigenfunctions
.
Notice that the zeroth-order term vanished because of the BCs.
(This expansion is continued in Appendix I).
A general sum of scaling eigenfunctions
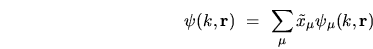 |
(6.5) |
is also a scaling wavefunction.
The tension (as defined in the previous chapter for Dirichlet BCs) of
a general scaling wavefunction is
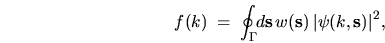 |
(6.6) |
where
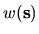 is a boundary weighting function.
If
is a boundary weighting function.
If 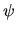 is now written in the form (6.5) then
the tension is
is now written in the form (6.5) then
the tension is
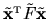 .
The matrix
.
The matrix 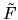 is the scaling eigenfunction
representation of the tension quadratic form, and we will see that it has
wonderful properties.
For
is the scaling eigenfunction
representation of the tension quadratic form, and we will see that it has
wonderful properties.
For
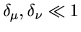 we can substitute (6.4)
as follows,
we can substitute (6.4)
as follows,
where 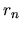 is an abbreviation for
is an abbreviation for
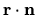 at the location
at the location 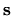 .
The final form has been written in terms of the boundary
inner-product matrix of the
eigenstate normal derivatives,
.
The final form has been written in terms of the boundary
inner-product matrix of the
eigenstate normal derivatives,
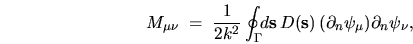 |
(6.8) |
where
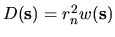 is the weight defining the inner-product.
The approximation
is the weight defining the inner-product.
The approximation
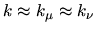 has been used, because
has been used, because
 has only very slow dependence on
has only very slow dependence on 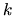 .
Note that all the fast dependence of
.
Note that all the fast dependence of 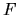 on
on 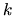 appears in the
wavenumber shifts
appears in the
wavenumber shifts 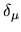 and
and 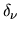 .
.
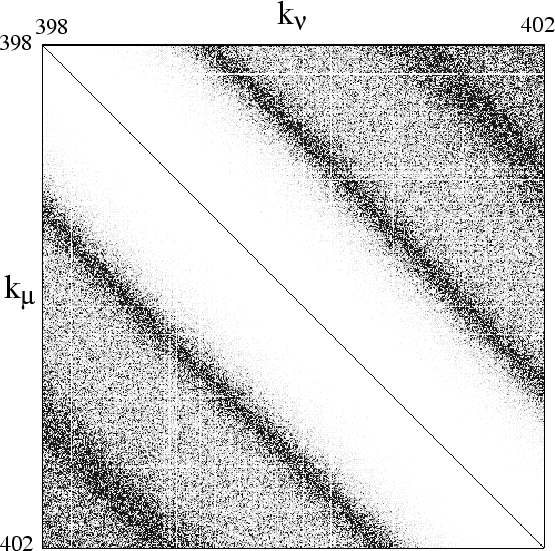
Figure:
Image of the matrix
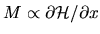 shown as a density plot
of
shown as a density plot
of
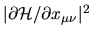 ,
for the case of dilation (a special deformation) of the 2D quarter
stadium billiard.
Darker pixels correspond to larger values.
The wide central white region (of width
,
for the case of dilation (a special deformation) of the 2D quarter
stadium billiard.
Darker pixels correspond to larger values.
The wide central white region (of width
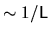 )
corresponds to quasi-orthogonality: the quantum
band profile vanishes like
)
corresponds to quasi-orthogonality: the quantum
band profile vanishes like 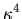 as
as
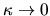 ,
where
,
where
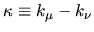 .
The diagonal is unity, and is not included in the band profile.
The matrix involves all 451 eigenstates falling in the
wavenumber range
.
The diagonal is unity, and is not included in the band profile.
The matrix involves all 451 eigenstates falling in the
wavenumber range 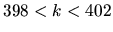 .
.
 |



Next: Quasi-orthogonality on the boundary
Up: The basic scaling method
Previous: The basic scaling method
Alex Barnett
2001-10-03
![]() is a Helmholtz solution at wavenumber
is a Helmholtz solution at wavenumber ![]() ,
then the rescaled version
,
then the rescaled version
![]() of the same wavefunction
obeys the Helmholtz equation at a new wavenumber
of the same wavefunction
obeys the Helmholtz equation at a new wavenumber ![]() :
:

![]() of the exact billiard eigenfunctions scaled as above to have
a single wavenumber
of the exact billiard eigenfunctions scaled as above to have
a single wavenumber ![]() ; these are called scaling eigenfunctions [195].
The unscaled eigenfunctions are taken to have unit normalization
in the billiard.
The index
; these are called scaling eigenfunctions [195].
The unscaled eigenfunctions are taken to have unit normalization
in the billiard.
The index
![]() labels the eigenfunctions in ascending order of
their unscaled wavenumber
labels the eigenfunctions in ascending order of
their unscaled wavenumber ![]() .
The scaling eigenfunctions no longer go to zero on the original billiard
boundary
.
The scaling eigenfunctions no longer go to zero on the original billiard
boundary ![]() , however they do go to zero on rescaled (dilated
or contracted) versions
of the boundary
, however they do go to zero on rescaled (dilated
or contracted) versions
of the boundary ![]() (see Fig. 6.1).
Imagine that a state
(see Fig. 6.1).
Imagine that a state ![]() has a wavenumber shift
has a wavenumber shift
![]() which is very small (
which is very small (
![]() , the inverse system size).
Then
, the inverse system size).
Then ![]() will be very close to
will be very close to ![]() , and the value of
, and the value of
![]() for
for
![]() will
be close to zero.
The boundary coordinate
will
be close to zero.
The boundary coordinate ![]() measures location on
measures location on ![]() .
Applying (6.3), the difference from zero is given by
.
Applying (6.3), the difference from zero is given by
