


Next: Solving for the scaling
Up: Representation in a Helmholtz
Previous: Linear function space at
Because the scaling eigenfunctions
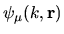 defined above all have
the same
defined above all have
the same 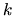 , and are normalizable, they fall into the above linear space.
They can be represented by
coefficient vectors
, and are normalizable, they fall into the above linear space.
They can be represented by
coefficient vectors
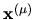 of a
Helmholtz basis set with a single wavenumber
of a
Helmholtz basis set with a single wavenumber 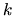 ,
,
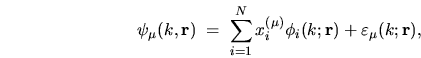 |
(6.17) |
where
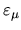 is some small error function for each state.
(The error function is a Helmholtz solution and is orthogonal to the basis
set space).
The functions
is some small error function for each state.
(The error function is a Helmholtz solution and is orthogonal to the basis
set space).
The functions 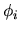 will not be orthogonal over
will not be orthogonal over 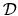 , and there will
be some (numerical) null-space of vectors
, and there will
be some (numerical) null-space of vectors 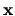 that has negligible effect
on wavefunctions inside
that has negligible effect
on wavefunctions inside 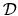 (see Section 5.3.1).
(see Section 5.3.1).
The boundary tension 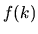 is a quadratic form
in the linear space.
Applying this form to the error
is a quadratic form
in the linear space.
Applying this form to the error
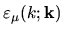 gives the
achievable tension minimum
gives the
achievable tension minimum 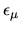 for each state.
In the
for each state.
In the 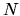 -dimensional above basis, the quadratic form is written
-dimensional above basis, the quadratic form is written
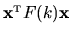 where
where 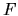 is the tension matrix.
is the tension matrix.
In the methods of the previous chapter the only requirement on the
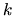 -dependence of this basis set was that at a given
-dependence of this basis set was that at a given 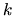 all the functions
are Helmholtz solutions at that
all the functions
are Helmholtz solutions at that 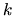 .
In this chapter we must specialize to a scaling basis,
.
In this chapter we must specialize to a scaling basis,
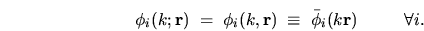 |
(6.18) |
Note that
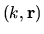 implies a scaling function whereas
implies a scaling function whereas
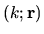 implies
some more general
implies
some more general 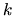 -dependence.
The expansion of any scaling function, as in (6.17), now has a
coefficient vector
-dependence.
The expansion of any scaling function, as in (6.17), now has a
coefficient vector 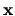 which is constant as
which is constant as 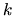 changes.
This will be necessary for our particular case of the
scaling eigenfunctions.
Note that certain basis sets, most notably that of the BIM, cannot be
used because their basis functions
(Green's functions) have origins at different points
`pinned' to the boundary
changes.
This will be necessary for our particular case of the
scaling eigenfunctions.
Note that certain basis sets, most notably that of the BIM, cannot be
used because their basis functions
(Green's functions) have origins at different points
`pinned' to the boundary 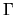 .
.



Next: Solving for the scaling
Up: Representation in a Helmholtz
Previous: Linear function space at
Alex Barnett
2001-10-03
![]() defined above all have
the same
defined above all have
the same ![]() , and are normalizable, they fall into the above linear space.
They can be represented by
coefficient vectors
, and are normalizable, they fall into the above linear space.
They can be represented by
coefficient vectors
![]() of a
Helmholtz basis set with a single wavenumber
of a
Helmholtz basis set with a single wavenumber ![]() ,
,
![]() is a quadratic form
in the linear space.
Applying this form to the error
is a quadratic form
in the linear space.
Applying this form to the error
![]() gives the
achievable tension minimum
gives the
achievable tension minimum ![]() for each state.
In the
for each state.
In the ![]() -dimensional above basis, the quadratic form is written
-dimensional above basis, the quadratic form is written
![]() where
where ![]() is the tension matrix.
is the tension matrix.
![]() -dependence of this basis set was that at a given
-dependence of this basis set was that at a given ![]() all the functions
are Helmholtz solutions at that
all the functions
are Helmholtz solutions at that ![]() .
In this chapter we must specialize to a scaling basis,
.
In this chapter we must specialize to a scaling basis,