Alex Barnett
Welcome! Here is my CV, and below is some news about mentees and collaborators.
To find out about my research and contact details,
and research of colleagues, see the
Center for Computational Mathematics, Flatiron Institute, Simons Foundation, and the
Numerical Analysis area.
Research topics at CCM include signal processing, numerical PDE, numerical analysis, fast algorithms, biophysics, fluids, waves, data analysis, computational statistics, deep learning, sampling, optimization, protein imaging, inverse problems, quantum simulation, neuroscience tools, and software libraries.
We accept postdoc (FRF) applications each Fall.
Many of my papers are on
arXiv, most are in
google scholar; also see outreach and education.
Research and teaching pre-2017 is also listed in a local copy of my former academic page as a professor of mathematics at Dartmouth College.
You can find some of my numerical software projects on
github
and on CCM's
software page.
I encourage high-quality submissions to the journal Advances in Computational Mathematics (ACOM),
for which I am co-Editor in Chief with Karsten Urban. I was a guest editor for this topical collection on integral equations.
In 2019 I was the main organizer for Flatiron-Wide Algorithms and Mathematics (FWAM)
which had three similar blockbuster sequels.
Meetings: Wednesdays at 10am we have the
CCM Colloquium / Group Meeting.
Tuesdays at 10am we have Scientific Computing Seminar.
Recent research images/movies
Some images click to play movie (MP4)... or see old Dirichlet Laplace eigenfunctions (|φj|2 for half-mushroom, quarter-stadium)
|
|
|
|
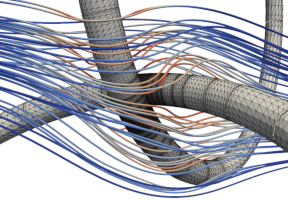
3D Stokes flow lines solved near slender rigid bodies separated by 1/20 of their minor radius, computed to 10-digit accuracy using CSBQ (with D. Malhotra; arxiv '23).
|
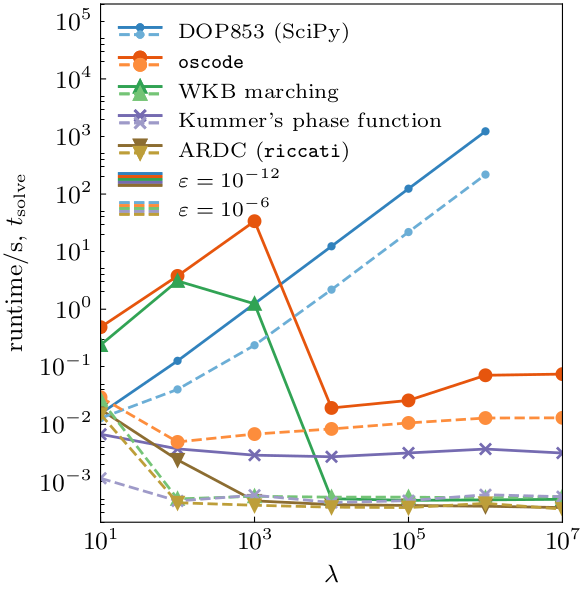
Timings of our ARDC solver vs others,
for a 2nd-order oscillatory ODE with frequency λ,
via adaptive defect correction for the Riccati phase function
(with F. Agocs; SINUM '23)
|
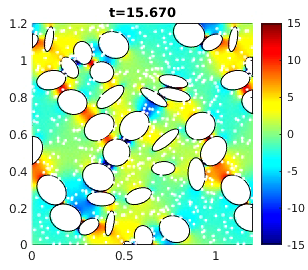
2D periodic rheology simulation via boundary integral equations: 25 rigid neutrally-buoyant ellipses per unit cell in a shearing Stokes flow (with J. Wang, E. Nazockdast; JCP '21)
|
News, talk slides, and outreach
- My paper with
Fruzsina Agocs
on adaptive Riccati defect correction for frequency-independent solution of oscillatory 2nd-order linear ODEs, was accepted by SINUM.
- See a blog-post style GitHub repo comparing two fast spectral methods for the Poisson equation in the square, with Dan Fortunato.
- Fruzsina Agocs
presented a poster on our joint work on acoustic scattering
and trapping on periodic surfaces (with applications to the raindrop effect at ancient Mayan staircases) at FACM23, NJIT, 5/26/23.
- May 2023: Our paper on iterated quadrature for Brillouin zone integrals in
quantum physics was accepted at SciPost Physics.
- April 2023: Congratulations to postdoc mentee Dan Fortunato on his ARS appointment at Flatiron, joint between CCM and CCB.
-
Courant Institute (NYU), 11/11/22: Equispaced Fourier representations for efficient Gaussian process regression from a billion data points (submitted to SIAM/ASA J. Uncert. Quant.; analysis results to ACHA). Joint work with Philip Greengard, Manas Rachh. Also given at Dartmouth College, Yale, and Imperial College.
- May 2022: Postdoc mentee Fruzsina Agocs presented our joint work An adaptive spectral method for oscillatory second-order linear ODEs with frequency-independent cost (submitted to SIAM J. Numer. Anal.), at CMO (Oaxaca). She presented more recent versions at NJIT, Chicago, NYU, Yale, and SIAM CSE23.
Check out her
riccati Python package.
-
CMO workshop (Oaxaca, Mexico), 5/26/22:
Challenges in fast solvers for highly oscillatory problems (short overview).
- July 2022: Congratulations to former intern Yu-Hsuan (Melody) Shih
[GH]
on receiving her PhD at NYU and moving to a new job as a senior software engineer working on math libraries at nVidia.
- April 2022: Congratulations to postdoc mentee Jason Kaye on his ARS appointment at Flatiron, joint between CCQ and CCM.
-
Flatiron-Wide Algorithms and Mathematics (FWAM3), 10/14/21:
Joys and pitfalls of numerical computing
(accompanying MATLAB/Octave demo codes:
pisqsix.m,
bigpca.m,
stoch.m,
linsys.m
)
- SIAM Annual Meeting, online (minisymposium 57), 7/21/21: Fresnel diffraction for starshade design using the non-uniform FFT.
- ICOSAHOM, online (minisymposium 27a), 7/12/21: Quadrature by fundamental solutions: kernel-independent layer potential evaluation for large collections of simple objects. Work with David Stein (CCB).
- Congratulations to first author (and former CCM intern) Yu-hsuan (Melody) Shih for the Best Paper Award PDSEC-21 for our paper on cuFINUFFT. Here's her 20-min talk video.
- Congratulations to postdoc mentee Jun Wang on her tenure-track job in math at Tsinghua University.
- Our work on SpikeForest (paper) and spike sorting featured on the Neural Implant Podcast, thanks to Jeremy Magland and James Jun, 3/16/20.
- Princeton PACM Seminar, 2/3/20:
Building a better non-uniform fast Fourier transform.
- Flatiron-Wide Algorithms and Mathematics (FWAM), 10/30/19:
Introduction to interpolation, integration, and spectral methods (see Lecture I; lecture II by Keaton Burns).
- Mathematical Fluids, Materials and Biology, U. Michigan, 6/14/19:
Fast boundary integral solvers for Stokes flows: quadrature, periodization, adaptivity.
- SIAM CSE, Spokane, WA, 3/1/19: Overview of high-order Nyström surface quadratures for fast solvers (review talk).
- Random geometries / Random topologies, ETH Zürich, 12/4/17:
Experimental Nazarov-Sodin constants, genus, and percolation on nodal domains for 2D and 3D random waves
(given remotely to save CO2).
Other links
