The vector Finite Element Method

Figure 8.5: A transverse magnetic field component is represented by a patchwork of bilinear (i.e. lowest-order) basis functions, each living a rectangle, covering the $x{-}y$ plane.

The technique represents the electric and magnetic fields as simple piecewise functions over many ``elements'' (regions) subdividing a slice through the guide and surrounding media in the xy plane, therefore by a finite number of degrees of freedom (see Fig. 8.4.1). Each element has a dielectric constant associated with it, allowing arbitrary stepwise refractive index distributions in the xy plane to be modelled. Maxwell's equations for propagating solutions of the form $\exp(ik_z z - i\omega t)$ are reduced to a generalized sparse eigenvalue equation with $k_z^2$ as the eigenvalue and the bound mode field distributions as the eigenvectors. For introductory reviews of electromagnetic waveguide bound-mode techniques see Silvester and Ferari [182] and Davies [56].

Specifically, we used the technique of Fernandez and Lu [139], with $H_x$ and $H_y$ as the field degrees of freedom, for simplicity using first-order (bilinear) functions to represent these fields over each element in a two-dimensional grid. To reach a compromise between flexibility and ease of coding, the grid of elements was chosen to be non-uniform (in order to allow high densities in the regions where fields changed rapidly, and low densities in others), but rectangular and separable into a product of elements in the x and y directions. See Fig. 8.4.1 which shows an example grid used for calculation.

This required a generalization of the Fernandez and Lu implementation, and careful consideration of their line-integral terms (which are non-standard for a finite element formulation). Of the many available finite element approaches to dielectric waveguide mode solution, this frequency-domain method was chosen for its absence of `spurious modes' (unphysical numerical solutions), its ability to handle index step discontinuities, its small number of required degrees of freedom, and its matrix sparsity. It does not perform as well as some more complicated methods which represent more field degrees of freedom (for a comparison of some current methods, see [178]).

Rather than emulating a radiative boundary condition (a notoriously hard task usually requiring an additional outer iterative loop, due to the $k_z$ dependence of the boundary condition), we enclosed the problem in a large, perfectly-conducting box of sufficient size that the bound mode evanescent fields were negligible on its walls, rendering the exact nature of the boundary condition irrelevant. However, the average level spacing of the unbound modes (the `continuum') decreases with increasing box size, and especially near cut-off we found that this increases the number of iterations required to solve the eigenvalue problem to a given accuracy. Thus we have a trade-off, and found that a box size of $6\lambda$ to $7\lambda$ gave the best compromise between accuracy and speed.

Figure 8.6: Finite elements in the $x{-}y$ plane: an example rectangular, non-uniform but separable grid used for calculation. The grid fills a box, which is chosen to be large enough that the fields on its boundary are negligible.

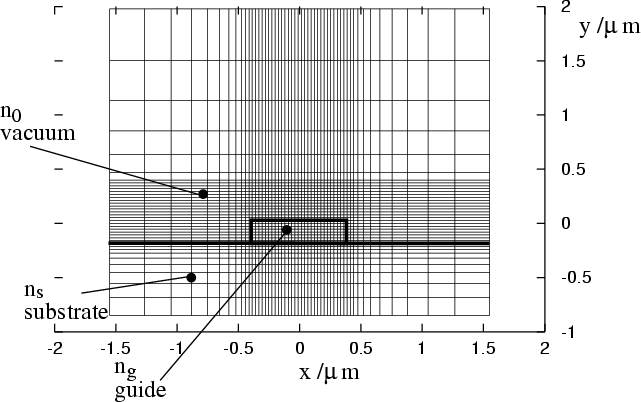We used the well-known ARPACK nonsymmeteric sparse eigenvalue solver [133] (essentially a block Lanczos [81,125] iterative solver) to find the 11 lowest eigenmodes of the sparse matrix. Of these, only the lowest 4 were needed to identify the single-mode region in Fig. 8.2, and only the lowest 2 eigenvectors were needed for their electric field information. Our non-uniform elements allowed us to have a high element density across the waveguide and in the adjacent trapping region, but a low density over the much larger box area, keeping the total number of degrees of freedom manageable.