


Next: Convergence with number of
Up: Dissipation in Deforming Chaotic
Previous: Appendix F: Cross correlations
Appendix G: Numerical evaluation of wavefunction boundary integrals
Boundary methods are a central component of this thesis.
Closed integrals of a function
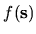 over the boundary coordinate
over the boundary coordinate 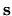 are ubiquitous.
Generally
are ubiquitous.
Generally
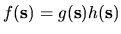 and
a square
matrix
and
a square
matrix 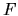 of integrals
of integrals
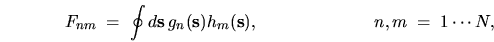 |
(G.1) |
is required, where the indices label multiple functions.
For evaluation of the quantum band profile (Chapters 2 and
3),
the local density of states (Chapter 6),
the tension and area-norm matrices (Chapter 5), and
the Vergini matrix
and its derivative (Chapter 6),
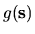 and
and
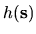 are basis functions or eigenstates
which oscillate about zero on the length scale
are basis functions or eigenstates
which oscillate about zero on the length scale
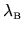 , the quantum
(de Broglie) free-space wavelength.
The deformation function boundary integrals (Chapter 4)
do not involve any quantum scale, but are also evaluated using the method
below.
I will present only the
, the quantum
(de Broglie) free-space wavelength.
The deformation function boundary integrals (Chapter 4)
do not involve any quantum scale, but are also evaluated using the method
below.
I will present only the 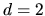 case where boundary integrals over
case where boundary integrals over 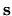 become
line integrals over
become
line integrals over 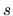 ; the generalization to higher
; the generalization to higher 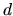 is simple.
is simple.
My tool for evaluation of an integral on a closed curve is the
discretization
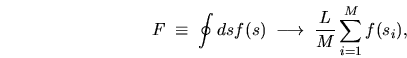 |
(G.2) |
where 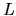 is the range of
is the range of 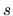 , that is, the length of the line integral
(billiard perimeter).
The
, that is, the length of the line integral
(billiard perimeter).
The 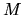 points are spread uniformly (equidistant in
points are spread uniformly (equidistant in 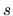 )
along the closed curve.
Because no point is special, no special quadrature [161]
weights arise near any endpoints: all weights are equal.
More sophisticated and accurate approximations
exist for closed line integral
evaluation [58], however this is sufficient for my needs
and is very simple to code.
Its errors will be discussed and tested below.
)
along the closed curve.
Because no point is special, no special quadrature [161]
weights arise near any endpoints: all weights are equal.
More sophisticated and accurate approximations
exist for closed line integral
evaluation [58], however this is sufficient for my needs
and is very simple to code.
Its errors will be discussed and tested below.
A single integral (G.2) requires 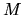 function evaluations of
function evaluations of 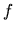 .
Naively one might guess that filling a matrix
.
Naively one might guess that filling a matrix 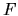 using (G.1)
requires
using (G.1)
requires 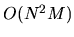 evaluations.
However, the correct way to compute (G.1) requires only
evaluations.
However, the correct way to compute (G.1) requires only
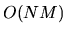 such evaluations:
First fill the rectangular matrices
such evaluations:
First fill the rectangular matrices
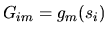 and
and
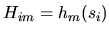 , from which follows
, from which follows
 |
(G.3) |
This matrix multiplication does require 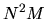 operations, but being
simple adds and multiplications (and using optimized library code
e.g. BLAS), it is very fast and does not affect the scaling.
If you like, the matrix multiply `performs' the integration over
operations, but being
simple adds and multiplications (and using optimized library code
e.g. BLAS), it is very fast and does not affect the scaling.
If you like, the matrix multiply `performs' the integration over 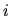 .
In the case where
.
In the case where 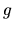 and
and 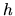 are the same function, only
are the same function, only 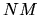 evaluations
are required.
Note that if a general weighting function
evaluations
are required.
Note that if a general weighting function
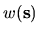 is required in the
integrand (G.1), it can easily be incorporated into
is required in the
integrand (G.1), it can easily be incorporated into 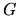 or
or 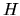 ,
or equivalently be included as a diagonal matrix
,
or equivalently be included as a diagonal matrix 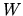 inserted between
inserted between
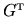 and
and 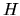 in (G.3).
in (G.3).
Subsections



Next: Convergence with number of
Up: Dissipation in Deforming Chaotic
Previous: Appendix F: Cross correlations
Alex Barnett
2001-10-03
![]() over the boundary coordinate
over the boundary coordinate ![]() are ubiquitous.
Generally
are ubiquitous.
Generally
![]() and
a square
matrix
and
a square
matrix ![]() of integrals
of integrals
![]() function evaluations of
function evaluations of ![]() .
Naively one might guess that filling a matrix
.
Naively one might guess that filling a matrix ![]() using (G.1)
requires
using (G.1)
requires ![]() evaluations.
However, the correct way to compute (G.1) requires only
evaluations.
However, the correct way to compute (G.1) requires only
![]() such evaluations:
First fill the rectangular matrices
such evaluations:
First fill the rectangular matrices
![]() and
and
![]() , from which follows
, from which follows