In this chapter I describe a numerical method for finding billiard eigenstates which involves `sweeping' the energy to locate the states. It is a generalization of and improvement upon Heller's Plane Wave Decomposition Method (PWDM) [90,91]. The PWDM was invented over 15 years ago and provided a more powerful and rapid way to find eigenstates in certain billiard shapes than had been available beforehand. In this chapter several problems of the PWDM have been solved (missing states, sensitivity to choice of basis set size and number of matching points), it has been simplified, the accuracy is improved, and the speed has been increased considerably. This chapter is also a useful introduction to the following one, where a much more efficient method (which bypasses the `sweep' altogether) is analysed.
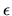for truncation
