


Next: A) `Basis diagonalization'
Up: Introduction and history of
Previous: General definitions
Almost all interesting quantum problems involve 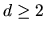 degrees of freedom.
Almost invariably in this case
the wavefunction
degrees of freedom.
Almost invariably in this case
the wavefunction 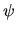 is represented by a
linear sum of basis functions,
is represented by a
linear sum of basis functions,
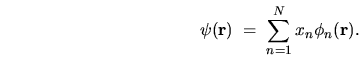 |
(5.4) |
This is computationally necessary since it reduces the function
space of 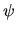 to a finite number
to a finite number 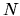 of degrees of freedom, namely the coefficient vector
of degrees of freedom, namely the coefficient vector 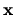 .
For a complete basis, any
.
For a complete basis, any
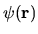 can be exactly represented by
(5.4) in the limit
can be exactly represented by
(5.4) in the limit
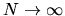 .
Clearly a computer can only handle finite
.
Clearly a computer can only handle finite 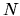 , so the basis should be
well chosen so that sufficient convergence is achieved for the
, so the basis should be
well chosen so that sufficient convergence is achieved for the
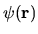 of interest with a manageable
of interest with a manageable 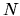 .
The choice of basis falls into two general classes:
(A) The basis does not depend on
.
The choice of basis falls into two general classes:
(A) The basis does not depend on 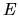 , or
(B) the basis does depend on
, or
(B) the basis does depend on 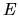 .
This results in two general strategies, summarized in Table 5.1
and now discussed in detail below.
The nomenclature ``Class A'' etc which I introduce here is new to the literature.
.
This results in two general strategies, summarized in Table 5.1
and now discussed in detail below.
The nomenclature ``Class A'' etc which I introduce here is new to the literature.
Subsections



Next: A) `Basis diagonalization'
Up: Introduction and history of
Previous: General definitions
Alex Barnett
2001-10-03
![]() degrees of freedom.
Almost invariably in this case
the wavefunction
degrees of freedom.
Almost invariably in this case
the wavefunction ![]() is represented by a
linear sum of basis functions,
is represented by a
linear sum of basis functions,