


Next: Categories of existing numerical
Up: Introduction and history of
Previous: Introduction and history of
When the Hamiltonian of a quantum mechanical problem
is independent of time,
the time evolution of the quantum state (wavefunction)
can always be written as the
sum of components with harmonic time-dependence.
Each component, or stationary state, 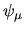 ,
is a solution of the time-independent Schrodinger equation
(TISE)
,
is a solution of the time-independent Schrodinger equation
(TISE)
 |
(5.1) |
The (hermitian) operator 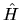 is linear, so we have a linear eigenproblem,
which only has solutions for (real) energies
is linear, so we have a linear eigenproblem,
which only has solutions for (real) energies 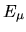 .
If we ignore all discrete quantum numbers (spin)
then
.
If we ignore all discrete quantum numbers (spin)
then 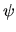 is a function of continuous variables only
which can be written generally as a vector
is a function of continuous variables only
which can be written generally as a vector 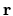 .
The dynamical variable
.
The dynamical variable 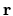 may represent the location of a particle, or
many particles, or more general coordinates such as relative distances,
angles, etc.
One can define position states
may represent the location of a particle, or
many particles, or more general coordinates such as relative distances,
angles, etc.
One can define position states
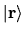 which are the eigenstates of
the position operator
which are the eigenstates of
the position operator
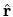 , and which form a complete basis
for the quantum problem.
, and which form a complete basis
for the quantum problem.
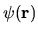 is the position representation of the wavefunction,
and
is the position representation of the wavefunction,
and
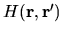 is the position representation of
is the position representation of 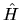 .
If
.
If 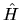 is local, as is the case in a huge variety of physical
situations,
then
is local, as is the case in a huge variety of physical
situations,
then
![$H({\mathbf r},{\mathbf r}') = \delta({\mathbf r}-{\mathbf r}') [h_0({\mathbf r}') +
h_1({\mathbf \nabla}_{{\mathbf r}'}) + \cdots]$](img649.gif) is a function
only of the local value and spatial derivatives of the wavefunction.
The function
is a function
only of the local value and spatial derivatives of the wavefunction.
The function 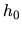 is commonly known as the potential.
For instance a very common form of Hamiltonian arising in the case of
isotropic mass
is commonly known as the potential.
For instance a very common form of Hamiltonian arising in the case of
isotropic mass 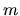 and quadratic dispersion relation is
and quadratic dispersion relation is
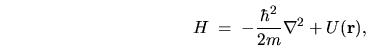 |
(5.2) |
written as an operator in the position representation.
The potential is
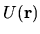 .
However, when
.
However, when 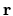 does not simply indicate location of a single particle
in a conservative potential,
then (5.2) is not sufficiently general.
does not simply indicate location of a single particle
in a conservative potential,
then (5.2) is not sufficiently general.
If the Hamiltonian is infinite (or much larger than the energies of interest)
outside a finite region, then
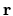 is effectively confined to this region and
the eigenenergies
is effectively confined to this region and
the eigenenergies 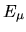 are discrete.
This is also true if
are discrete.
This is also true if 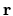 is not strictly confined, but if the energy
is below the continuum transition[128], giving bound states.
In this latter case
is not strictly confined, but if the energy
is below the continuum transition[128], giving bound states.
In this latter case 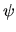 can take non-zero values over an infinite
region of
can take non-zero values over an infinite
region of 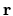 ; however outside
a certain
(classically-allowed) region
the decay is exponential so the effective region of confinement is finite.
I will be interested in solving for these resulting discrete states.
The problem is to find the eigenvalues
; however outside
a certain
(classically-allowed) region
the decay is exponential so the effective region of confinement is finite.
I will be interested in solving for these resulting discrete states.
The problem is to find the eigenvalues 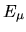 ,
or equivalently the eigenfunctions
,
or equivalently the eigenfunctions
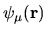 , for which (5.1)
is obeyed.
If an
, for which (5.1)
is obeyed.
If an 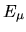 is known then it is easy to get the corresponding
is known then it is easy to get the corresponding
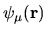 ,
and vice versa.
If there is no analytical solution, then a numerical approach
is required--the subject of this and following chapters.
,
and vice versa.
If there is no analytical solution, then a numerical approach
is required--the subject of this and following chapters.
The issue of boundary conditions (BCs) now enters; notice that
it is not actually present in the eigenproblem (5.1).
BCs arise because of the computational need to consider only
a finite region.
The finite region is chosen such that
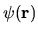 is negligible outside the
region.
I call the region
is negligible outside the
region.
I call the region 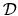 and its boundary
and its boundary 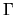 (see Fig. 5.1).
If
(see Fig. 5.1).
If
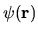 dies smoothly to zero (as is true for a smooth-potential
or soft-walled problem), then the choice of
dies smoothly to zero (as is true for a smooth-potential
or soft-walled problem), then the choice of 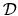 is determined
by the required accuracy.
The smallest region
is determined
by the required accuracy.
The smallest region 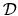 is found
such that
is found
such that
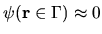 to a sufficient approximation.
In this case, the exact nature of BCs imposed at
to a sufficient approximation.
In this case, the exact nature of BCs imposed at 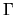 is irrelevant
for the problem--the only important BC is then the
asymptotic restriction
is irrelevant
for the problem--the only important BC is then the
asymptotic restriction
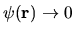 with increasing distance outside the finite region.
Another class of problems results if the potential suddenly changes (for instance
if it jumps to infinity corresponding to a hard wall) at the edge of the
problem region.
It is then natural to locate
with increasing distance outside the finite region.
Another class of problems results if the potential suddenly changes (for instance
if it jumps to infinity corresponding to a hard wall) at the edge of the
problem region.
It is then natural to locate 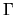 at this edge (often this
is essential since it avoids the difficulty of representing
singularities which occur at the edge).
Therefore
at this edge (often this
is essential since it avoids the difficulty of representing
singularities which occur at the edge).
Therefore 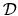 , and the BCs at
, and the BCs at 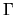 , are exactly specified.
To summarize,
the BCs result from truncation of the region of space to
, are exactly specified.
To summarize,
the BCs result from truncation of the region of space to
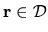 .
.
BCs can generally be written
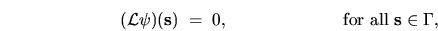 |
(5.3) |
where 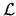 is a linear operator which acts on the function space of
is a linear operator which acts on the function space of
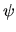 , and is sensitive only to its values, gradients,
and higher derivatives, at the boundary
, and is sensitive only to its values, gradients,
and higher derivatives, at the boundary 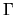 .
The result of the operator is the smaller function space
of functions of the boundary position coordinate
.
The result of the operator is the smaller function space
of functions of the boundary position coordinate 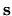 .
Generally
.
Generally 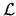 is local on
is local on 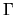 , meaning it measures only
properties of
, meaning it measures only
properties of
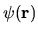 local to a point
local to a point
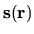 .
For instance, most BCs are described by special cases of the operator
.
For instance, most BCs are described by special cases of the operator
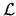 which returns a
(position-dependent) linear combination of the local value and normal gradient
(this is known as `mixed BCs').
which returns a
(position-dependent) linear combination of the local value and normal gradient
(this is known as `mixed BCs').
BCs may be specified for other reasons.
They may enter in the context of solving for resonance states in the continuum,
where they can model the effect of an infinite region of space
whose propagator is known analytically.
These ``radiative BCs'' may be non-local on 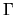 , and the resulting
, and the resulting
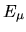 will be complex.
The calculation of eigenstates in the continuum (which are usually
highly degenerate) is a scattering problem, and
I shall not consider it further.
Also the eigenstates in a region with certain BCs can be needed for use in
other methods, for instance R-matrix theory[131] for
scattering problems.
will be complex.
The calculation of eigenstates in the continuum (which are usually
highly degenerate) is a scattering problem, and
I shall not consider it further.
Also the eigenstates in a region with certain BCs can be needed for use in
other methods, for instance R-matrix theory[131] for
scattering problems.
Figure:
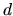 dimensional domain
dimensional domain 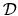 and
and
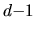 dimensional boundary
dimensional boundary 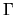 of a quantum solution region.
The local normal
of a quantum solution region.
The local normal
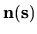 is also shown.
is also shown.
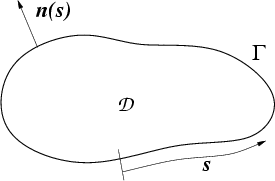 |
Table 5.1:
Two general classes of quantum eigenproblem solution strategies using
basis sets.
The desired solutions are the eigenenergies 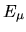 and the states
(written in terms of basis coefficients)
and the states
(written in terms of basis coefficients)
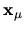 .
For other physical wave eigenproblems, the TISE (5.1)
should be replaced by
the appropriate time-independent
wave equation obeyed in the domain (e.g. Helmholtz equation).
In the methods of this chapter a diagonalization will replace the SVD
(singular value decomposition).
The scaling method of Vergini and Saraceno (not listed) combines
the best elements of both
classes.
.
For other physical wave eigenproblems, the TISE (5.1)
should be replaced by
the appropriate time-independent
wave equation obeyed in the domain (e.g. Helmholtz equation).
In the methods of this chapter a diagonalization will replace the SVD
(singular value decomposition).
The scaling method of Vergini and Saraceno (not listed) combines
the best elements of both
classes.
| |
(A) `basis diagonalization' |
(B) `Green's function matching' |
| |
|
|
| basis |
Independent of 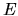 . . |
Depend on 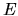 . . |
| funcs. |
Obey BCs. |
Don't obey BCs. |
| |
Don't obey TISE. |
Are solutions of TISE. |
| |
|
|
| basis size |
Scales like volume of 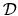 |
Scales like surface area
of 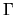 |
| |
|
|
| technique |
Write TISE in terms of basis |
Write BC matching equations |
| |
coefficients. |
in terms of basis coefficients |
| |
|
and boundary locations. |
| |
|
|
| resulting |
|
|
| equation |
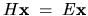 |
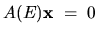 |
| |
|
|
| |
Diagonalization of 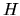 matrix matrix |
Hunt in 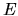 for for
![$\det [A(E)] = 0$](img664.gif) , needs , needs |
| |
finds many
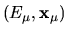 at once. at once. |
many SVDs per
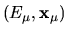 found. found. |
| |
|
|
| examples |
Finite Element Method |
Boundary Integral (or Element) |
| |
(FEM)[19]. |
Method (BIM or BEM)[121]. |
| |
Discrete-Variable |
Plane Wave Decomposition |
| |
Representation (DVR)[17]. |
Method (PWDM) of Heller
[91]. |
| |
Discretization on a lattice[161]. |
Bogomolny's method[34]. |
| |
Robnik conformal mapping[171]. |
Lupu-Sax t-matrix inversion[140]. |
| |
|
Methods of this chapter. |
| |
|
|
|



Next: Categories of existing numerical
Up: Introduction and history of
Previous: Introduction and history of
Alex Barnett
2001-10-03
![]() ,
is a solution of the time-independent Schrodinger equation
(TISE)
,
is a solution of the time-independent Schrodinger equation
(TISE)
![]() is effectively confined to this region and
the eigenenergies
is effectively confined to this region and
the eigenenergies ![]() are discrete.
This is also true if
are discrete.
This is also true if ![]() is not strictly confined, but if the energy
is below the continuum transition[128], giving bound states.
In this latter case
is not strictly confined, but if the energy
is below the continuum transition[128], giving bound states.
In this latter case ![]() can take non-zero values over an infinite
region of
can take non-zero values over an infinite
region of ![]() ; however outside
a certain
(classically-allowed) region
the decay is exponential so the effective region of confinement is finite.
I will be interested in solving for these resulting discrete states.
The problem is to find the eigenvalues
; however outside
a certain
(classically-allowed) region
the decay is exponential so the effective region of confinement is finite.
I will be interested in solving for these resulting discrete states.
The problem is to find the eigenvalues ![]() ,
or equivalently the eigenfunctions
,
or equivalently the eigenfunctions
![]() , for which (5.1)
is obeyed.
If an
, for which (5.1)
is obeyed.
If an ![]() is known then it is easy to get the corresponding
is known then it is easy to get the corresponding
![]() ,
and vice versa.
If there is no analytical solution, then a numerical approach
is required--the subject of this and following chapters.
,
and vice versa.
If there is no analytical solution, then a numerical approach
is required--the subject of this and following chapters.
![]() is negligible outside the
region.
I call the region
is negligible outside the
region.
I call the region ![]() and its boundary
and its boundary ![]() (see Fig. 5.1).
If
(see Fig. 5.1).
If
![]() dies smoothly to zero (as is true for a smooth-potential
or soft-walled problem), then the choice of
dies smoothly to zero (as is true for a smooth-potential
or soft-walled problem), then the choice of ![]() is determined
by the required accuracy.
The smallest region
is determined
by the required accuracy.
The smallest region ![]() is found
such that
is found
such that
![]() to a sufficient approximation.
In this case, the exact nature of BCs imposed at
to a sufficient approximation.
In this case, the exact nature of BCs imposed at ![]() is irrelevant
for the problem--the only important BC is then the
asymptotic restriction
is irrelevant
for the problem--the only important BC is then the
asymptotic restriction
![]() with increasing distance outside the finite region.
Another class of problems results if the potential suddenly changes (for instance
if it jumps to infinity corresponding to a hard wall) at the edge of the
problem region.
It is then natural to locate
with increasing distance outside the finite region.
Another class of problems results if the potential suddenly changes (for instance
if it jumps to infinity corresponding to a hard wall) at the edge of the
problem region.
It is then natural to locate ![]() at this edge (often this
is essential since it avoids the difficulty of representing
singularities which occur at the edge).
Therefore
at this edge (often this
is essential since it avoids the difficulty of representing
singularities which occur at the edge).
Therefore ![]() , and the BCs at
, and the BCs at ![]() , are exactly specified.
To summarize,
the BCs result from truncation of the region of space to
, are exactly specified.
To summarize,
the BCs result from truncation of the region of space to
![]() .
.
![]() , and the resulting
, and the resulting
![]() will be complex.
The calculation of eigenstates in the continuum (which are usually
highly degenerate) is a scattering problem, and
I shall not consider it further.
Also the eigenstates in a region with certain BCs can be needed for use in
other methods, for instance R-matrix theory[131] for
scattering problems.
will be complex.
The calculation of eigenstates in the continuum (which are usually
highly degenerate) is a scattering problem, and
I shall not consider it further.
Also the eigenstates in a region with certain BCs can be needed for use in
other methods, for instance R-matrix theory[131] for
scattering problems.
