


Next: The hunt for local
Up: The choice of norm
Previous: Estimation by interior points
It is possible to calculate 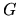 exactly using
exactly using 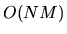 basis function
(or derivative) evaluations.
The equivalent expressions (H.14) and (H.7)
both give the domain overlap of two Helmholtz solutions
(with no particular BCs) at the same wavenumber,
purely in terms of boundary integrals.
Taking for example the former expression, it can be approximated
(using the discretization of Appendix G) as
basis function
(or derivative) evaluations.
The equivalent expressions (H.14) and (H.7)
both give the domain overlap of two Helmholtz solutions
(with no particular BCs) at the same wavenumber,
purely in terms of boundary integrals.
Taking for example the former expression, it can be approximated
(using the discretization of Appendix G) as
![\begin{displaymath}
G \; = \; \frac{{\mathsf{A}}}{M} \, \frac{1}{2k^2} \left[
...
... - (A^{{\mbox{\tiny T}}} B + B^{{\mbox{\tiny T}}} A) \right] ,
\end{displaymath}](img791.gif) |
(5.20) |
where the four rectangular matrices are defined by
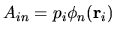 ,
,
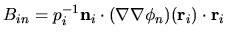 ,
,
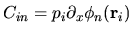 , and
, and
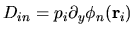 .
At each boundary point
.
At each boundary point 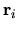 for
for 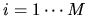 , the weight is
, the weight is
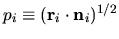 .
The outward normal at this point is
.
The outward normal at this point is 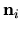 .
Notice that the (Hessian) matrix of second derivatives is required for
.
Notice that the (Hessian) matrix of second derivatives is required for  .
.
This formidable expression has been coded and tested. It has been found
that for the Dirichlet eigenproblem, it can be replaced by a much
simpler form which is valid only when the wavefunctions in question
vanish on the boundary, namely (H.9).
When written in a basis this gives
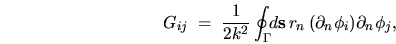 |
(5.21) |
where 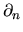 means derivative in the normal direction.
The discretized version is therefore
means derivative in the normal direction.
The discretized version is therefore
 |
(5.22) |
where
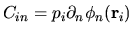 .
The largest few resulting generalized eigenvalues
.
The largest few resulting generalized eigenvalues 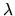 (and eigenfunctions) of
(5.14) are indistiguishable from those resulting from
(5.20).
That this works is not entirely obvious, because the basis functions
(and eigenfunctions) of
(5.14) are indistiguishable from those resulting from
(5.20).
That this works is not entirely obvious, because the basis functions 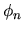 do not vanish on the boundary.
However all the relevant vectors
do not vanish on the boundary.
However all the relevant vectors 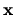 contain combinations of basis
functions which are very small on the boundary.
For the tension plots in this chapter, (5.22) has been used.
contain combinations of basis
functions which are very small on the boundary.
For the tension plots in this chapter, (5.22) has been used.
As a bonus, the eigenstates with Neumann BCs are to be found at the
minima of the smallest 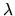 .
This is true because exchanging Dirichlet for Neumann in the tension
function definition is equivalent to swapping
.
This is true because exchanging Dirichlet for Neumann in the tension
function definition is equivalent to swapping 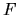 and
and 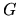 in
(5.14).
in
(5.14).



Next: The hunt for local
Up: The choice of norm
Previous: Estimation by interior points
Alex Barnett
2001-10-03
![]() exactly using
exactly using ![]() basis function
(or derivative) evaluations.
The equivalent expressions (H.14) and (H.7)
both give the domain overlap of two Helmholtz solutions
(with no particular BCs) at the same wavenumber,
purely in terms of boundary integrals.
Taking for example the former expression, it can be approximated
(using the discretization of Appendix G) as
basis function
(or derivative) evaluations.
The equivalent expressions (H.14) and (H.7)
both give the domain overlap of two Helmholtz solutions
(with no particular BCs) at the same wavenumber,
purely in terms of boundary integrals.
Taking for example the former expression, it can be approximated
(using the discretization of Appendix G) as
![]() .
This is true because exchanging Dirichlet for Neumann in the tension
function definition is equivalent to swapping
.
This is true because exchanging Dirichlet for Neumann in the tension
function definition is equivalent to swapping ![]() and
and ![]() in
(5.14).
in
(5.14).