I choose a basis set composed entirely of solutions to (5.5)
in ![]() .
Therefore they are
.
Therefore they are ![]() -dependent (equivalently, energy-dependent),
and this means we are joining the Class B methods.
Since the basis functions do not obey the BCs we can choose the
BCs for which the analytic forms of the functions are simplest,
namely, free space.
The eigenfunctions can be chosen real-valued everywhere, so we can
choose entirely real basis functions.
Typical basis functions at wavenumber
-dependent (equivalently, energy-dependent),
and this means we are joining the Class B methods.
Since the basis functions do not obey the BCs we can choose the
BCs for which the analytic forms of the functions are simplest,
namely, free space.
The eigenfunctions can be chosen real-valued everywhere, so we can
choose entirely real basis functions.
Typical basis functions at wavenumber ![]() include:
Real Plane Waves (RPWs),
Evanescent Plane Waves (EPWs),
and angular momentum states (e.g. the singular
include:
Real Plane Waves (RPWs),
Evanescent Plane Waves (EPWs),
and angular momentum states (e.g. the singular ![]() ) based at various origins
(which if they are singular, must be outside
) based at various origins
(which if they are singular, must be outside ![]() , or placed on
, or placed on ![]() as in the BIM basis set).
Each of these forms is oscillatory with wavenumber
as in the BIM basis set).
Each of these forms is oscillatory with wavenumber ![]() .
Following Heller's PWDM, the `default' basis will be RPWs uniformly spaced
in angle, containing both sin and cos terms, and suitably symmetrized for
the billiard shape.
The basis size
.
Following Heller's PWDM, the `default' basis will be RPWs uniformly spaced
in angle, containing both sin and cos terms, and suitably symmetrized for
the billiard shape.
The basis size ![]() will be discussed below.
Helmholtz basis sets will be further discussed in Sections 5.3.1 and
6.1.3, and examples described in
Appendix J.
will be discussed below.
Helmholtz basis sets will be further discussed in Sections 5.3.1 and
6.1.3, and examples described in
Appendix J.
Substitution of the ![]() -dependent basis representation
-dependent basis representation
The condition (5.12) is equivalent [7] to
finding the maximum-eigenvalue solution to the generalized
eigenproblem
Essentially, the method proposed in this chapter is then searching for
local minima in the inverse largest eigenvalue of
(5.14), as a function of ![]() .
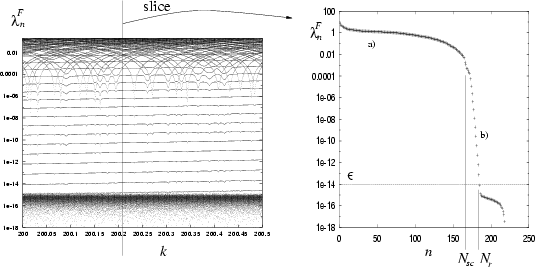
An example sweep in
.
An example sweep in ![]() is plotted in Fig. 5.2.
However there are implementation issues without which this specification
is all but useless.
The rest of the chapter is devoted to such issues.
is plotted in Fig. 5.2.
However there are implementation issues without which this specification
is all but useless.
The rest of the chapter is devoted to such issues.
 |
 |